Ca­pa­cité por­tante de ponts en arc en ma­çon­ne­rie

Les ponts en arc en maçonnerie constituent encore aujourd’hui une proportion étonnamment importante du parc des ouvrages européens. Précieux témoins de l’histoire, ils présentent généralement une capacité portante plus élevée que présumé, alliée à une très bonne durabilité lorsqu’ils sont bien entretenus (Grandjean, 2010).
Leur examen selon les normes SIA 269 (SIA, 2010) nécessite l’utilisation d’outils modernes permettant de tenir compte de toutes les réserves dont la structure dispose. Les méthodes disponibles jusqu’à aujourd’hui impliquaient l’utilisation de modèles numériques dont les résultats sont difficiles à contrôler, ou de modèles élastiques trop conservateurs. Les éléments structuraux annexes, tels que tympans ou culées, peuvent ensuite être examinés indépendemment.

La maçonnerie en tant que matériau

La maçonnerie est un matériau hétérogène et anisotrope, au comportement complexe. Ses propriétés dépendent des matériaux constitutifs (pierre et mortier), mais surtout de la manière dont ceux-ci sont assemblés (l’appareillage). Une étude du comportement de la maçonnerie, effectuée à l’aide d’un modèle numérique, a permis de définir les principaux critères de comportement du matériau (Grandjean, 2010). A l’échelle structurelle, la maçonnerie peut ainsi être assimilée à un matériau homogène, dont le comportement en compression suit une courbe contrainte-déformation parabolique et dont la résistance maximale à la compression varie entre 2 et 40 N/mm².

Mécanisme à quatre rotules

Le mode de ruine le plus probable d’un arc en maçonnerie, considéré comme une structure hyperstatique de degré 3, implique la formation d’un mécanisme résultant de l’apparition de rotules, au fur et à mesure de l’augmentation de la charge. Ce type de ruine, entraînant d’importantes redistributions plastiques, se traduit parune forte déformation de la structure.

Principe de formation de la rotule

Un arc est soumis à un effort de flexion composée (interaction effort normal-moment de flexion) équivalent à l’application d’un effort normal excentré. La résistance à la traction de la maçonnerie étant admise nulle, l’application d’un moment de flexion suffisant pour créer des tractions dans la section se traduit immédiatement par des fissures. Augmentant progessivement avec l’effort de flexion appliqué, leur ouverture s’accompagne d’une diminution graduelle de la section efficace disponible pour reprendre l’effort de compression, jusqu’à son écrasement en compression qui permet alors la formation d’une rotule.
Le modèle développé assimile cette rotule à une articulation mécanique qui autorise une rotation illimitée de deux portions d’arc considérées comme rigides. Il est en outre admis que cette section n’offre plus aucune résistance à l’imposition d’un moment de flexion supplémentaire, mais reste capable de transmettre un effort de compression considérable, grâce au confinement de la zone écrasée. Les faibles dimensions de la zone écrasée permettent par ailleurs d’admettre la rotule comme pratiquement réversible, donc d’envisager une modification de sa position sur l’arc en fonction de la charge variable appliquée.

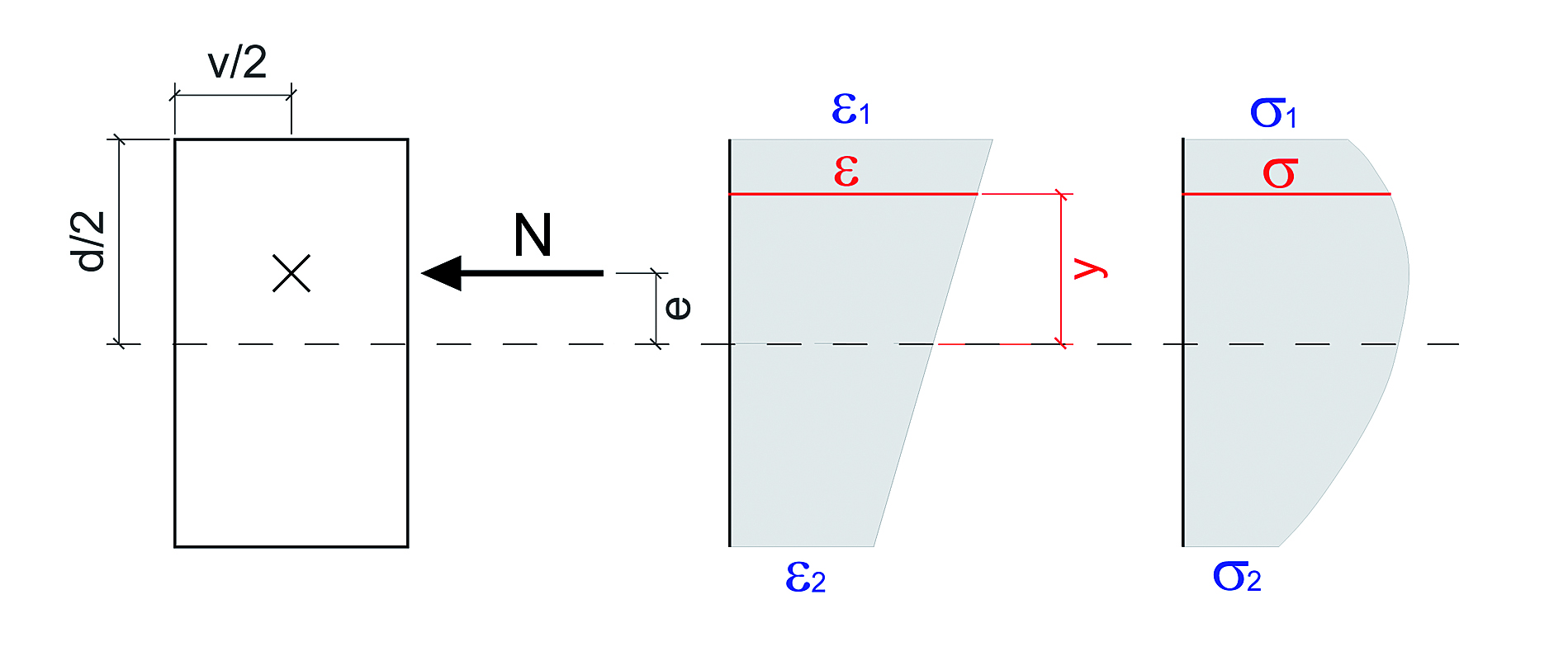
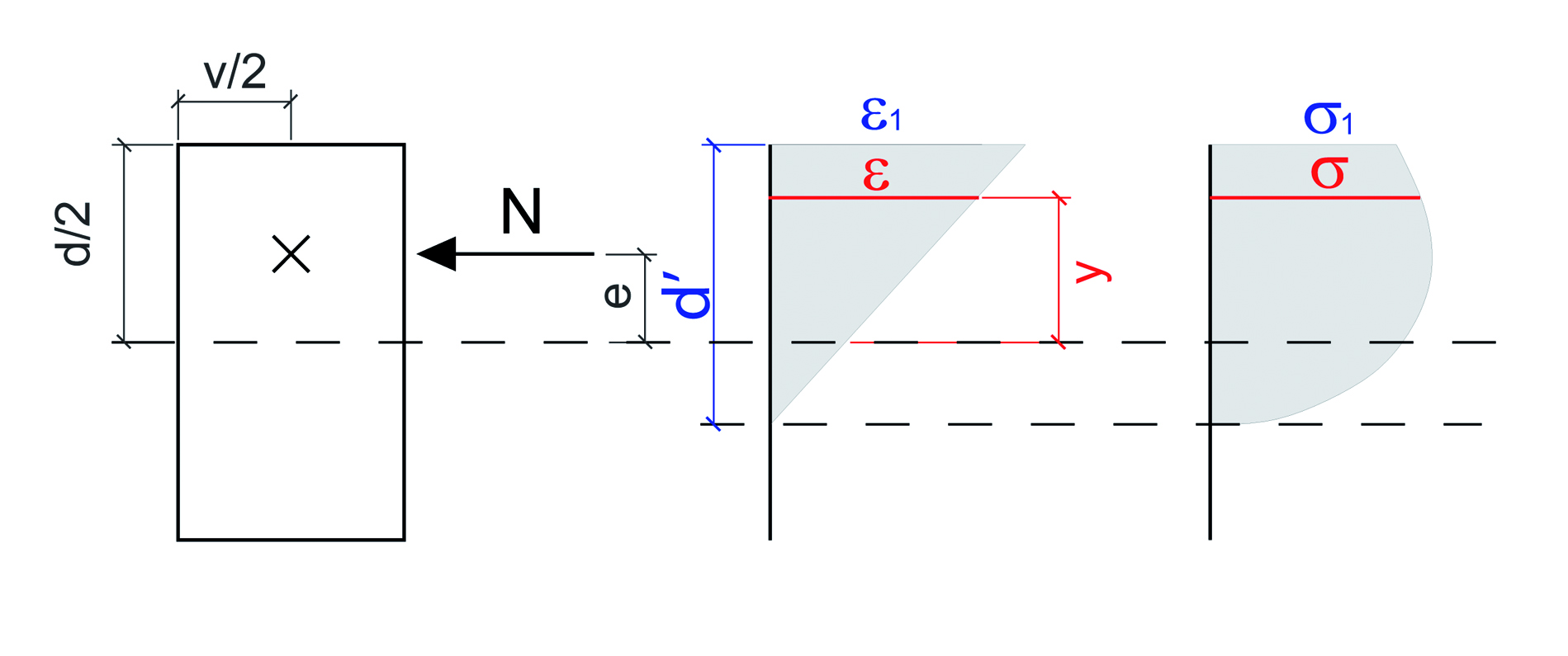
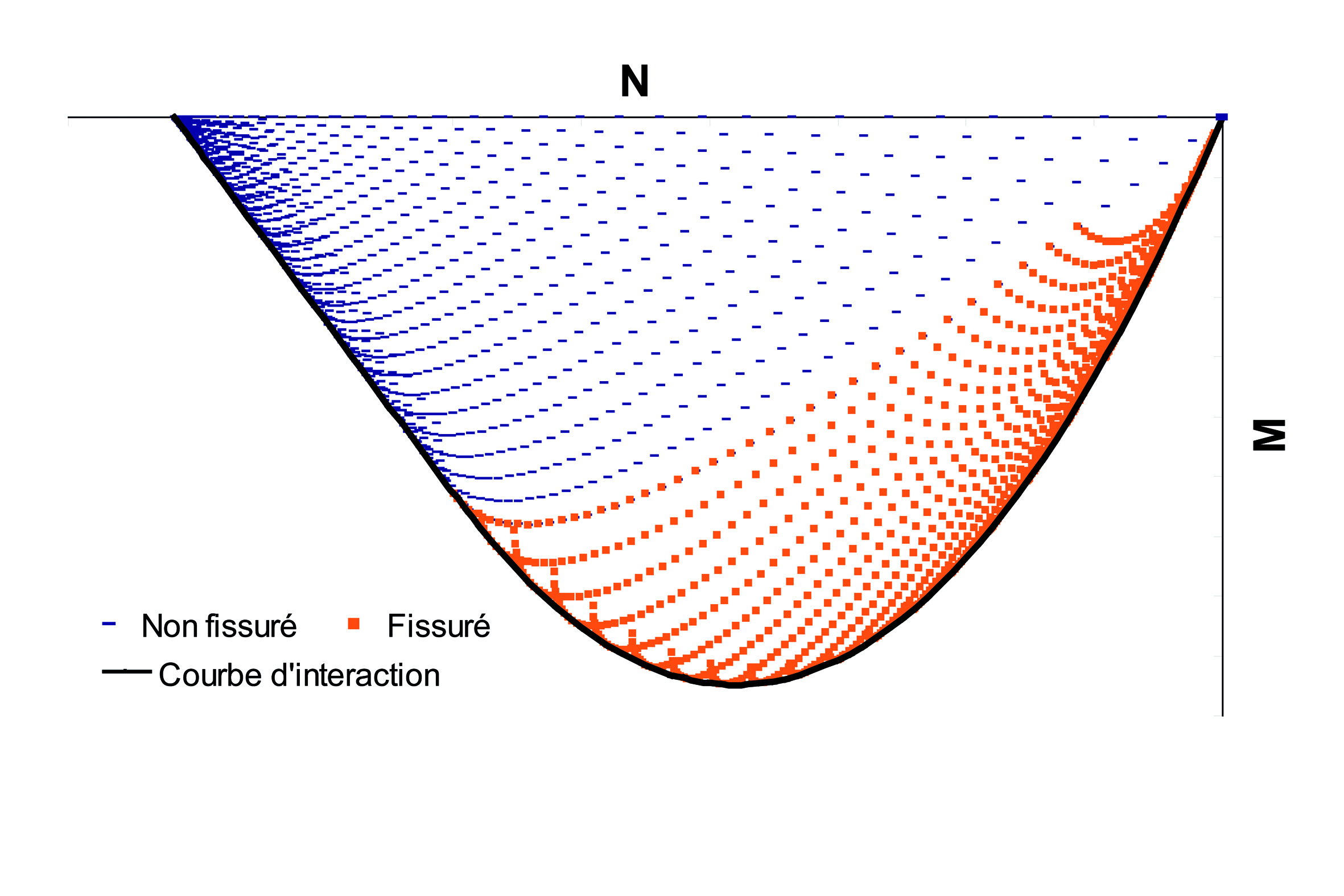
Diagramme d’interaction

Le comportement en compression simple de la maçonnerie,admise homogène, est défini par une courbe contrainte-déformation parabolique. L’hypothèse de Navier-Bernoulli concernant la conservation des sections planes permet de calculer, par intégration, l’ensemble des couples moment de flexion-effort normal admissibles pour la section et le matériau étudiés. Deux cas sont alors distingués, selon que la section est entièrement comprimée ou partiellement fissurée. Ces états de sollicitation admissibles sont rassemblés dans un diagramme d’interaction moment de flexion-effort normal. L’enveloppe de ces points – la courbe d’interaction – représente la résistance limite de la section considérée : chaque point de cette courbe correspond à une combinaison d’efforts susceptible de faire apparaître une rotule dans l’arc considéré.

Hypothèses et bases du modèle

Au vu du faible effort normal impliqué dans ce type de structures, une rupture par compression peut être d’emblée exclue ; tout comme celle induite par le glissement des voussoirs les uns par rapport aux autres, dont la vérification peut être effectuée de manière annexe, en admettant un frottement de Coulomb à l’interface pierre-mortier. L’arc peut alors être considéré comme un élément structurel bidimensionnel, bi-encastré, se ruinant suivant un mécanisme à quatre rotules.
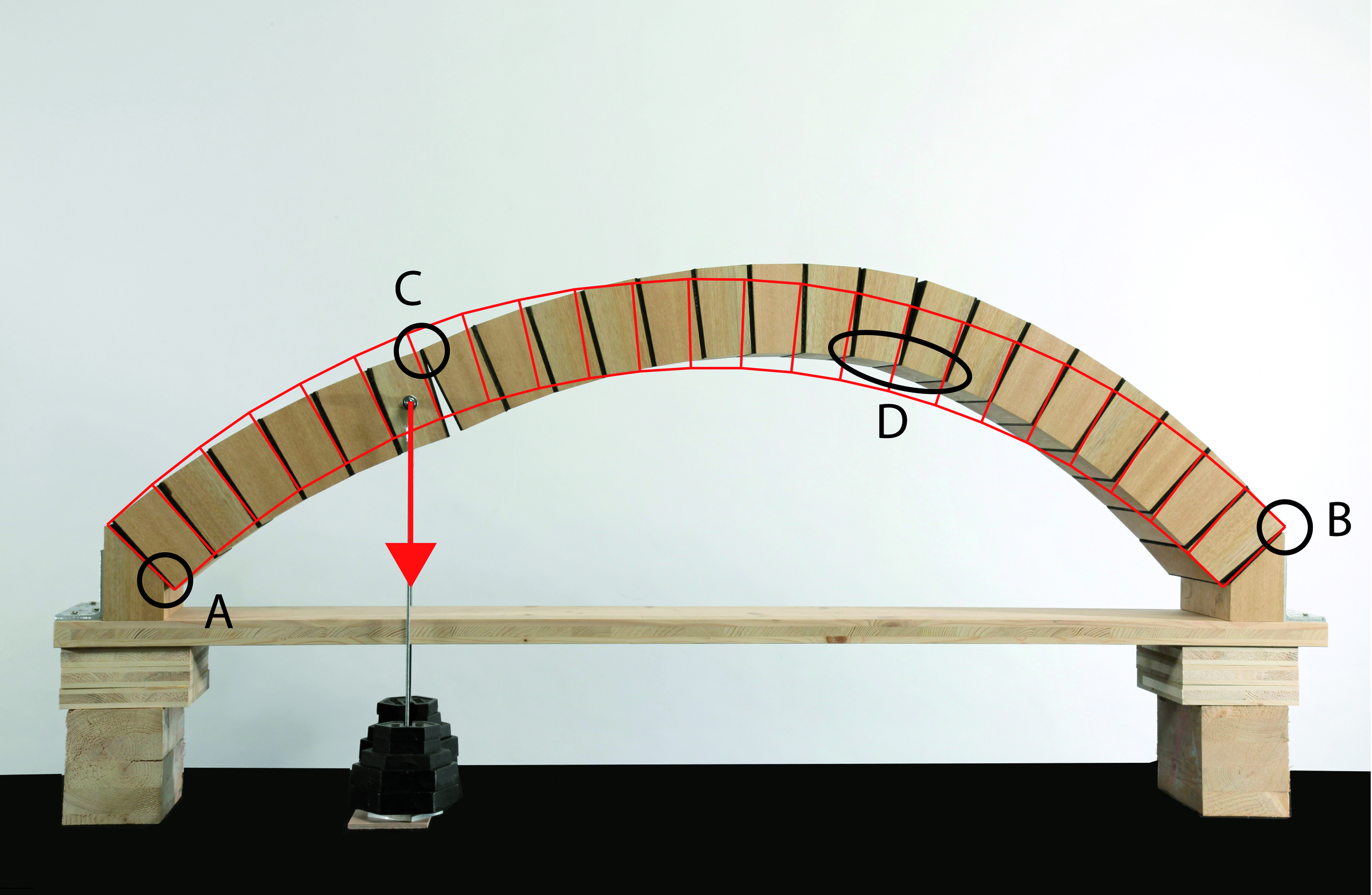
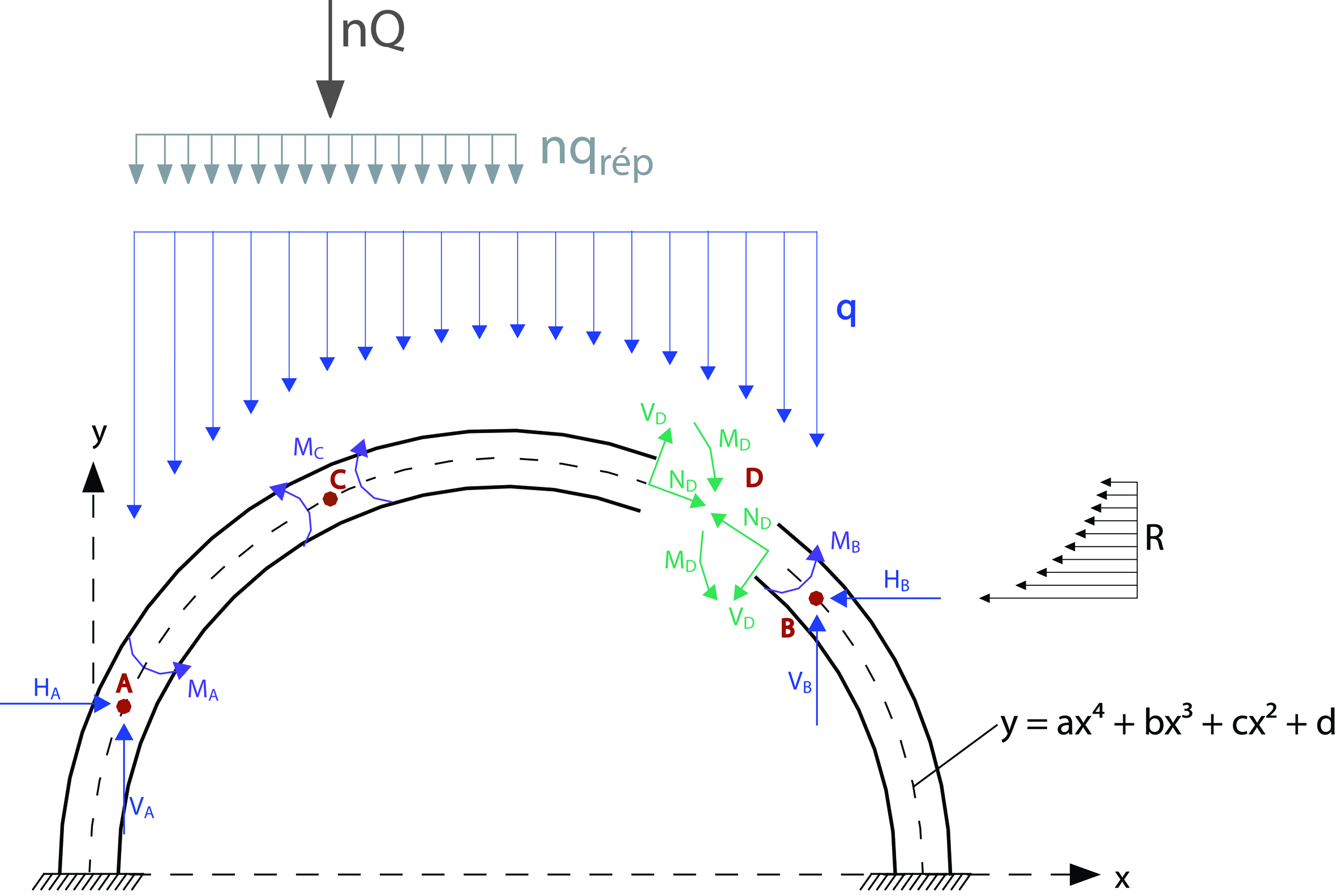
Le modèle développé considère l’arc lorsque trois rotules (A, B, et C) sont apparues, rendant la structure isostatique. Il est admis qu’elles se forment à l’axe de l’arc et leur position est, dans un premier temps, choisie à priori. En vertu de l’hypothèse de linéarité géométrique, le calcul peut se faire sur la configuration non déformée de l’arc. Sur chacune des trois rotules déjà formées est appliqué un moment de flexion extérieur (M_A, M_B et M_C), représentatif des efforts qui ont provoqué l’apparition de la rotule en ce point et qui correspondent à un point sur la courbe d’interaction précédemment déterminée. L’hyperstaticité de la structure fait qu’on ne peut connaître directement ces efforts et qu’il est nécessaire de les admettre à priori. Une étude complémentaire a prouvé que le choix d’une valeur identique pour les trois rotules – correspondant à un effort normal égal à 1250 kN sur le diagramme d’interaction – fournissait de bons résultats pour des arcs présentant des dimensions conventionnelles.
Bien que capables d’avoir un effet positif théorique sur la capacité portante de l’arc, la contribution des tympans est négligée : il a en effet été observé que ceux-ci se détachaient bien avant la ruine de l’arc, suite à l’apparition de deux fissures longitudinales à l’intrados de ce dernier.

Un modèle basé sur l’équilibre

Le tracé d’intrados de l’arc, qu’il soit semi-circulaire ou autre, est représenté par un polynôme de degré 4. Les charges permanentes considérées sont constituées par le poids propre du remplissage et de la voie de roulement q (le poids propre de l’arc est admis négligeable par rapport à celui du matériau de remplissage). Dans le cas d’un trafic routier, la charge variable prise en compte comprend une unique charge d’essieux ponctuelle Q, une configuration reconnue comme étant la plus dommageable pour les arcs en maçonnerie (un cas de charge ferroviaire peut être introduit de manière similaire). Cette charge est positionnée au droit de la rotule C et est complétée par une charge uniformément répartie q_rép sur la moitié de l’arc déjà sollicitée ponctuellement. Est aussi prise en compte une diffusion longitudinale et transversale de la charge répartie à travers le matériau de remplissage.
L’apparition des rotules conduit à une déformation de l’arc dont la portion située entre les rotules D et B subit un déplacement en direction du matériau de remplissage. 
Ce dernier exerce alors sur l’arc une poussée passive horizontale R, similaire à celle que produit un sol contre un mur de soutènement se déplaçant en direction du massif. Parfois ignorée, cette poussée peut avoir un effet positif non négligeable sur la stabilité de l’arc, mais son évaluation précise reste difficile. Elle est modélisée ici selon la théorie de Rankine, la valeur obtenue étant réduite par un facteur m_p afin de tenir compte de la courbure de l’arc et du déplacement potentiellement insuffisant de ce dernier pour mobiliser l’entier de l’effort. La poussée active agissant sur la partie opposée de l’arc est quant à elle négligée.
De simples considérations d’équilibre sur la structure – rendue isostatique par la présence des trois premières rotules – suffisent à calculer les efforts agissant en D, localisation choisie pour la future quatrième rotule. Un calcul inverse permet ensuite de déduire la charge utile qui provoquera les efforts suffisants pour plastifier la section D. La capacité portante de l’arc s’exprime alors par un facteur n, multiplicateur des charges de trafic (ponctuelle et répartie) initialement admises.
Basé sur le théorème cinématique de la plasticité (voir encadré), ce modèle fournit une borne supérieure de la solution réelle. Selon les principes de ce théorème, la solution réelle correspond au mécanisme fournissant la valeur minimale du multiplicateur des charges utiles n, qui doit alors être déterminée par itération sur la position des quatre rotules le long de l’arc.
Ce modèle peut facilement être implémenté dans un tableur type Excel, dont le solveur permet d’effectuer les itérations. Une fois établi, il pourra servir à l’évaluation de la capacité portante de tout arc en maçonnerie répondant aux hypothèses du modèle, les seules caractéristiques à introduire étant relatives aux matériaux mis en œuvre (maçonnerie et matériau de remplissage), à la géométrie de l’ouvrage et aux valeurs des charges variables admises.
Elaboré pour les ponts à portée unique, ce modèle s’applique à la majorité des ouvrages en maçonnerie. Une version étendue du modèle, applicable aux ponts à portées multiples, a par ailleurs également été développée. Il a été validé par son application à différents cas, les résultats obtenus ayant été comparés soit avec ceux fournis par un logiciel spécialisé, soit avec des résultats expérimentaux (Granjean, 2010)[1]. A titre d’exemple, le modèle développé a été appliqué au cas d’un pont construit en 1815, franchissant la Promenthouse près de Gland, dans le canton de Vaud. Un multiplicateur limite des charges utiles égal à 3,46 a été obtenu. Cette valeur, supérieure à l’unité, indique d’une part que la vérification de la sécurité structurale est satisfaite, et d’autre part qu’un modèle de charge de trafic 3,46 fois plus élevé que celui considéré pourrait être appliqué avant d’engendrer la ruine de l’arc.

Influence de l’endommagement

En raison de leur âge, et souvent suite à un manque d’entretien, les ponts anciens en maçonnerie présentent divers dommages (fissuration, matériau manquant, déformation). En comprendre les causes et l’influence réelle sur la capacité portante de la structure est essentiel pour limiter les interventions au maximum et préserver ainsi la valeur historique de l’ouvrage.
Trois cas de dommages fréquemment rencontrés ont été retenus et intégrés au modèle. Le premier cas consiste en une fissure longitudinale située à l’intrados de l’arc, plus ou moins au droit de la face interne des tympans. Elle résulte essentiellement de la poussée horizontale du matériau de remplissage contre les tympans. L’intégration de ce type de dommage dans le modèle peut se faire en réduisant la largeur disponible pour la diffusion latérale de la charge utile. L’application de ce modèle modifié, bien que basé sur des hypothèses conservatrices, montre que ce dommage n’a que très peu d’influence sur la capacité portante de l’arc.
Le second dommage examiné est provoqué par le déplacement des appuis de l’arc, lorsque ces derniers sont trop élancés ou insuffisamment fondés. Un tel déplacement fait naître trois rotules, et ce avant même l’application de toute charge utile. L’intégration de ce dommage dans le modèle se fait par la superposition de deux états de sollicitations. Le premier comprend l’arc tri-articulé, avec des moments appliqués dans chaque rotule (M_A, M_B et M_C), et sous l’effet des charges permanentes. Le second état de sollicitation agit également sur l’arc tri-articulé, mais sans appliquer des moments extérieurs dans les rotules et sous charge utile uniquement. Une fois les efforts en D calculés et superposés, la procédure est similaire à celle développée pour un arc non endommagé. Cette superposition signifie que l’apparition des trois premières rotules ne résulte que de l’application des charges permanentes, la charge utile ne contribuant qu’à la formation de la quatrième.
Le troisième cas consiste en un manque local de matériau qui définit une section préférentielle pour l’apparition d’une rotule. Sa prise en compte dans le modèle peut se faire en imposant d’une part la position d’une ou plusieurs rotules, et d’autre part en réduisant localement l’épaisseur efficace de l’arc, en fonction des constats effectués lors d’un relevé in situ.

Simple et transparent

Transparent, simple d’utilisation, le modèle proposé peut facilement être employé pour déterminer la sécurité structurale des ponts en maçonnerie, au sens des nouvelles normes SIA 269. L’intégration de l’état existant, par la prise en compte des dommages fréquemment rencontrés sur ce type de pont, permet une limitation des interventions nécessaires et favorise ainsi la préservation de la valeur historique de l’ouvrage.

Alix Grandjean est ingénieure civile, diplômée de l'Ecole polytechnique fédérale de Lausanne
Eugen Brühwiler est professeur et dirige le laboratoire de maintenance, construction et sécurité des ouvrages de l'Ecole polytechnique fédérale de Lausanne

La théorie de la plasticité

 

Les structures hyperstatiques atteignent la ruine après la plastification d’un nombre de sections égal à leur degré d’hyperstaticité plus 1. Ainsi, pour autant que ces plastifications ne se produisent pas toutes simultanément, l’hyperstaticité d’une structure permet de tenir compte de redistributions plastiques des efforts, et donc d’une réserve de résistance supplémentaire – et souvent conséquente – par rapport à un calcul élastique, qui admet une ruine dès l’apparition de la première plastification.
Les méthodes plastiques de recherche de la charge ultime s’appuient sur les deux théorèmes fondamentaux de l’analyse limite. Leur application nécessite que les charges extérieures augmentent proportionnellement les unes par rapport aux autres, que le comportement du matériau soit élasto-plastique et que la linéarité géométrique soit respectée.
Théorème statique : toute charge limite obtenue à partir d’une statique licite, à savoir respectant les conditions d’équilibre et de résistance des matériaux, est inférieure ou égale à la charge limite réelle.
Théorème cinématique : toute charge limite obtenue à partir d’une cinématique licite, à savoir respectant les conditions d’équilibre et de compatibilité cinématique du mécanisme choisi, est supérieure ou égale à la charge limite.
Un troisième théorème, dit d’unicité, stipule que la solution réelle est celle qui satisfait simultanément les conditions de statique et de cinématique licites.