Le for­me dell’equi­li­brio e la sta­ti­ca gra­fi­ca

Se l’architettura è l’arte dell’equilibrio, cioè se l’architetto-faber o l’architetto-costruttore ha a che fare con l’equilibrio, tale affermazione evoca diversi significati: il legame evidente, nelle radici dei termini latini, tra aequilibrium e aequitas, cioè tra architettura e etica; la ricerca dell’equilibrio nel processo progettuale; la valutazione dell’equilibrio tra il tutto e le parti dell’opera progettuale, come idea di concinnitas; gli equilibrismi dell’architetto che si destreggia fra cantiere, burocrazia, committenza; la ricerca dell’equilibrio tra le forze che agiscono sulla costruzione. Quest’ultima figura rimanda al valore tettonico dell’architettura e alla sua struttura, allo studio della forma più adatta (form finding) a resistere alle sollecitazioni e a scaricarle al suolo.¹

Il «problema strutturale» riferito alle costruzioni si fonda su alcune basi che regolano le «economie naturali»,² espresse dai principi dell’equilibrio e tradotte in economie statiche. Una data costruzione deve obbedire a un determinato quadro di economie statiche e offrire una certa fascia di garanzie di stabilità. Nello sviluppo delle discipline meccaniche, la Statica si occupa dell’equilibrio dei corpi in quiete; in particolare i due princìpi fondamentali della Statica dei cosiddetti sistemi rigidi si basano sul concetto di forze in equilibrio, azione e reazione, e di equilibrio tra momenti di forza. 

La Statica grafica è un metodo che utilizza delle tecniche grafiche per risolvere i problemi dell’equilibrio di un corpo rigido, permettendo di giungerne alla definizione attraverso la composizione o la scomposizione delle forze rappresentate in modo convenzionale. Alla base di tutta la statica grafica sta in effetti l’identificazione della forza con un segmento orientato, conquista quest’ultima che avviene in epoca moderna con l’ingresso del calcolo vettoriale.³ Prima di allora le forze non avevano una direzione e un verso. Lo stato di equilibrio di un sistema di corpi viene definito quando l’insieme delle forze e delle reazioni vincolari viene rappresentato con un poligono chiuso, il poligono delle forze. Il poligono funicolare è la costruzione fondamentale della statica grafica e traduce in linguaggio grafico le cosiddette equazioni cardinali della statica.

Da dove trae origine la trattazione di natura grafica dei metodi analisi per la valutazione della risultante di un sistema di forze agenti in un piano? Il padre fondatore è considerato Karl Culmann, tedesco di nascita e svizzero di professione. Dopo aver lavorato come ingegnere presso le ferrovie bavaresi ed essersi occupato delle tecniche costruttive per i nuovi ponti metallici, fu chiamato quale docente al Politecnico di Zurigo nel 1855 e si dedicò al suo voluminoso progetto di teorizzazione della statica grafica. Animato dalla convinzione che «il disegno fosse il linguaggio dell’ingegnere», ottenne risultati grafici per la soluzione di problemi legati alle travature reticolari, alla geometria delle masse e all’analisi delle strutture che ancor oggi sono patrimonio della meccanica delle strutture. Riuscì a utilizzare la geometria per risolvere problemi reali legati alla professione dell’ingegnere.

La sistematizzazione dei suoi studi viene pubblicata col titolo di Die Graphische Statik⁴ nel 1865. Vi appaiono due figure-chiave, il poligono delle forze (Kraftepolygon) e il poligono funicolare (Seilpolygon) per la soluzione del problema generale della determinazione degli sforzi.

«Le prime applicazioni sistematiche dei metodi grafici per la determinazione delle dimensioni delle diverse parti della costruzione sono dovute a Poncelet»,⁵ afferma Culmann nell’introduzione al suo voluminoso Traité de Statique graphique⁶ (tradotto in francese nel 1880), di cui riprendo la traduzione in italiano a opera di Edoardo Benvenuto (1980). Jean Victor Poncelet, ingegnere politecnico francese e docente all’École de l’artillerie et du genie di Metz dal 1825 al 1834, è riconosciuto da Culmann come precursore della statica grafica per i suoi studi sulla geometria di posizione (ora chiamata geometria descrittiva) e dei metodi grafici per il dimensionamento di volte e muri di sostegno. 

Tuttavia Poncelet non è il primo a cimentarsi nello studio dei problemi dell’equilibrio di un corpo in quiete con applicazioni a «figure funicolari». Simon Stevino,⁷ fiammingo, nel 1608 raccoglie le sue opere in un trattato a più volumi denominato Hypomnemata mathematica. Uno dei volumi tratta della Statica e in questo le considerazioni sull’equilibrio di due pesi collegati da funi e posti su due piani inclinati di pendenza diversa portano alla regola del parallelogramma delle forze. Deduce anche le tensioni in un poligono funicolare, preludendo alla statica grafica. Successivamente lo scienziato francese Pierre Varignon nella Nouvelle Mécanique,⁸ opera pubblicata postuma nel 1725, sviluppa la legge di composizione delle forze di Stevino e la regola del parallelogramma per la composizione delle forze e la determinazione della risultante, visualizzata attraverso un filo teso che agisce su una propria retta e a un certo momento risultante a seconda del punto del piano considerato (figura 1). I due concetti sottendono implicitamente alle leggi fondamentali della statica a garanzia dell’equilibrio. 

Le prime teorie statiche sull’arco in muratura sono sviluppate da Philippe de La Hire⁹ nel Traité de Mécanique (1730). Il problema dell’equilibrio di un tratto di fune, privo di peso, assoggettato a pesi diversi si attiene al comportamento dell’arco in quanto rovesciando la figura si ottiene proprio un arco a elementi compressi. D’altra parte l’equilibrio della fune (equilibrio funicolare) «è la più chiara espressione delle regole di composizione e decomposizione delle forze».¹⁰ 

I passaggi sopradescritti appartengono a quella che è stata definita la «preistoria»¹¹ della statica grafica, che hanno trovato fondamento in problemi tutt’altro che astratti sull’equilibrio. 

Con Culmann la statica grafica diventa disciplina autonoma che ben presto si diffonde in Europa e viene insegnata nelle maggiori scuole di Ingegneria, oltre che in Svizzera, nell’impero austroungarico, in Germania alla Gewerbe-Akademie e alla Bau-Akademie di Berlino e inoltre a Karlsruhe, Darmstadt, Monaco, Dresda, Hannover e Stoccarda; alla scuola politecnica di Riga per quanto riguarda la Russia dell’epoca; in Italia, dopo Milano (1860) e Padova (con il professor Favaro¹²), a Torino, Napoli, Palermo, Pisa, Bologna e Pavia;¹³ oltreoceano al MIT di Boston (con il professor Jerome Sondericker¹⁴).

Wilhelm Ritter (1847-1906), che succedette a Culmann nella cattedra di Scienza delle costruzioni di Zurigo, ne prosegue l’opera; i suoi studi furono inoltre ampliati da Mohr, Muller-Breslau, Lévy¹⁵ e Cremona con due metodi, l’uno che determina gli sforzi nelle aste a partire dallo studio dell’equilibrio in ogni sezione, l’altro a partire dall’equilibrio in ogni nodo. 

La diffusione della disciplina abbraccia la quasi totalità delle questioni che trattano dell’arte delle costruzioni (calcolo del centro di gravità e del momento d’inerzia, dimensionamento delle travi, degli archi, dei telai, studi sulla spinta delle terre e sulla stabilità dei muri ecc.).

Le applicazioni più feconde della statica grafica riguardano le travature reticolari, in quanto, come afferma Cremona, «la semplicità e la rapidità del metodo grafico, confrontato con i metodi algebrici, sono notevoli e non inducono a frequenti errori professionali»,¹⁶ come spesso accadeva.

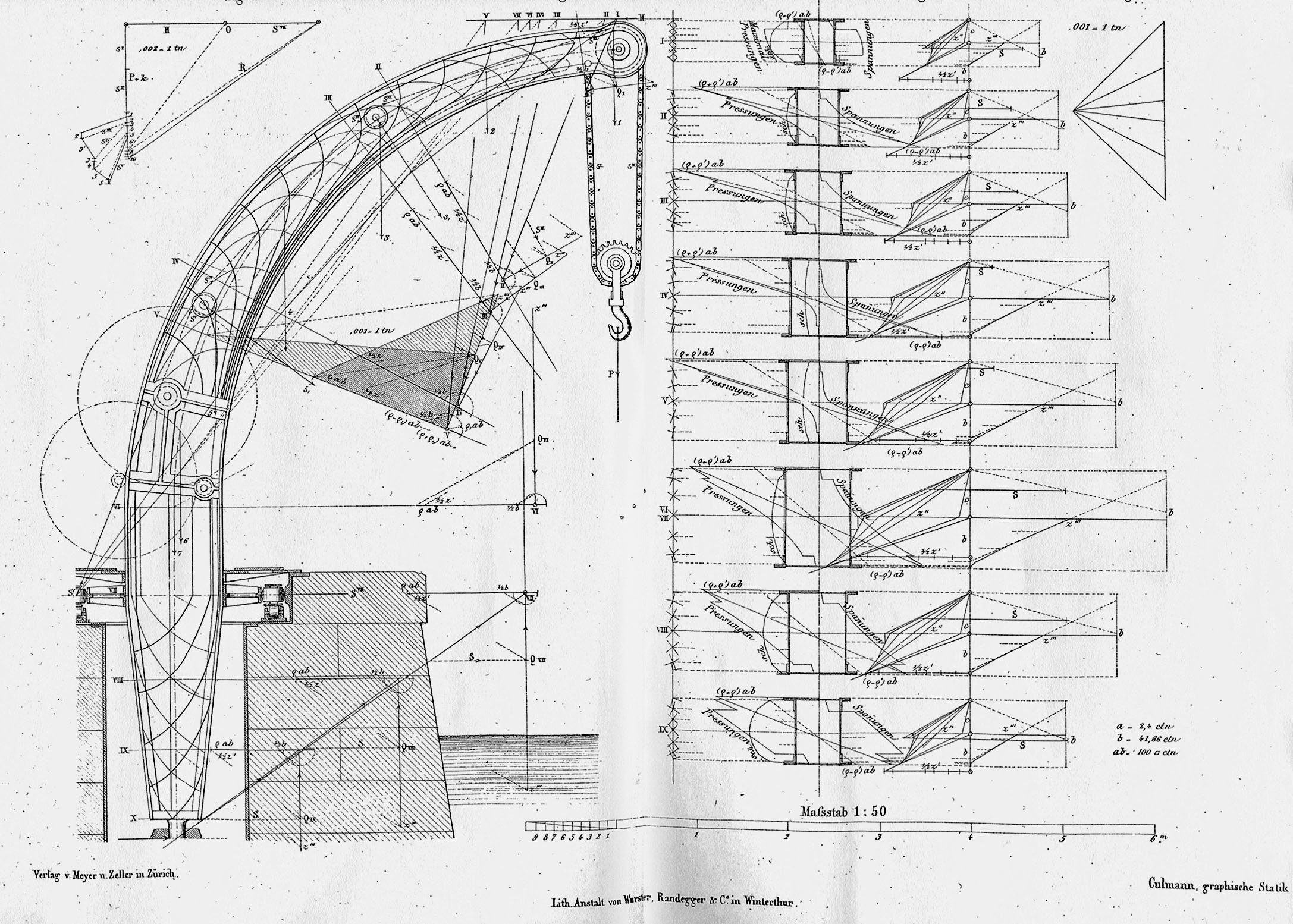
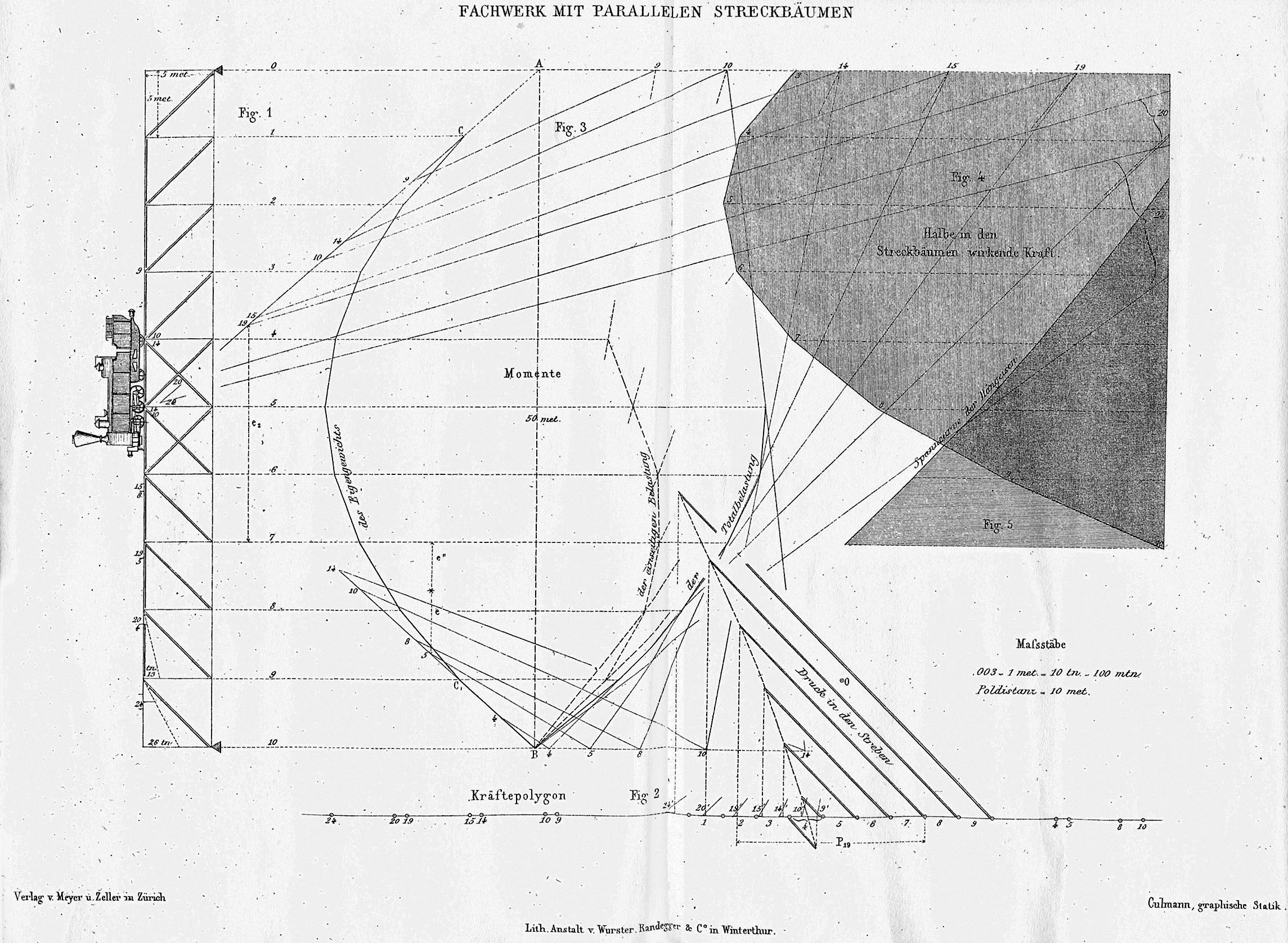
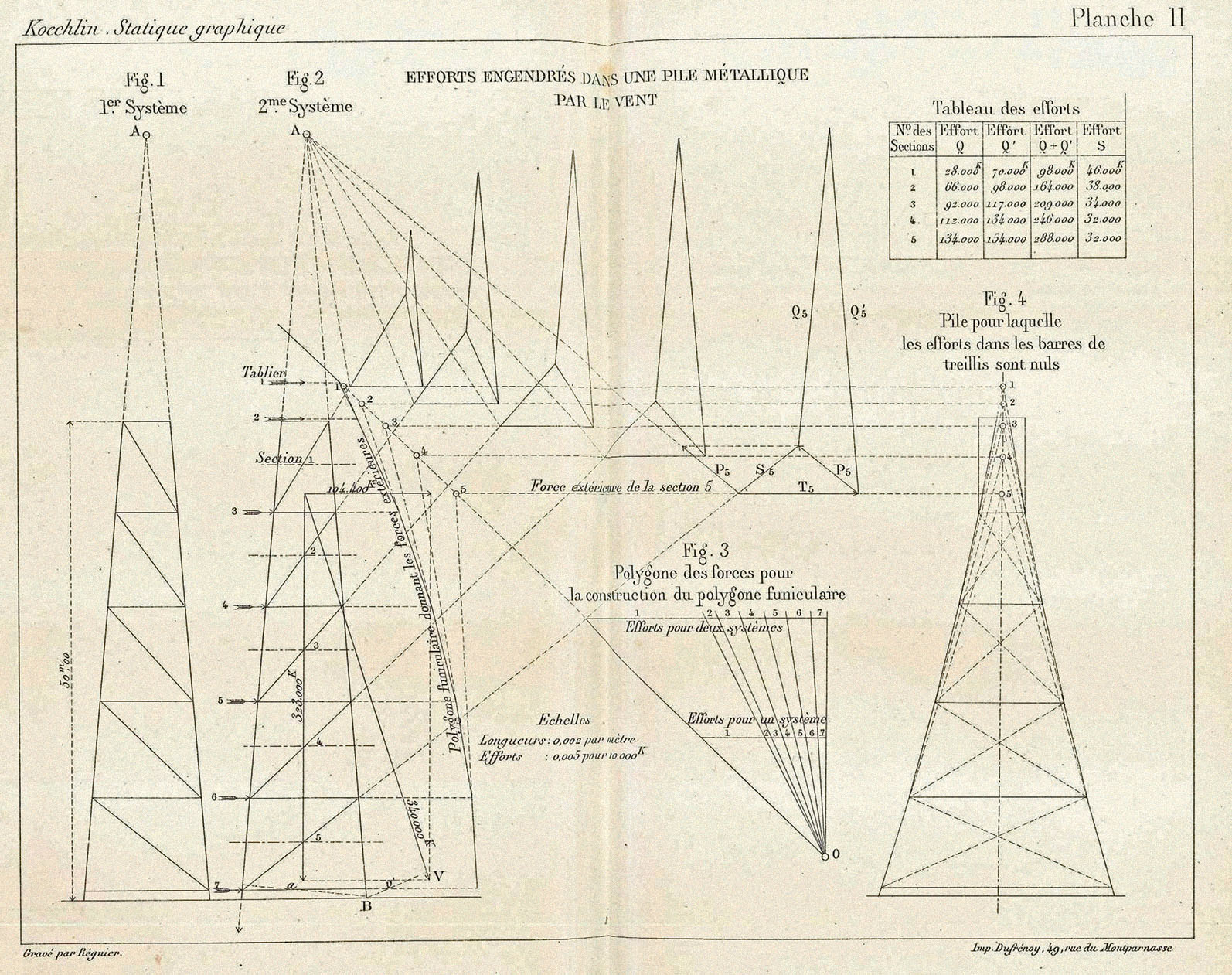
Nel suo trattato Culmann propone, tra l’altro, l’applicazione a un ponte ferroviario attraversato da una locomotiva, a un ponte sospeso, a un muro di sostegno e a una gru (figure %%gallerylink:5764:3%%, %%gallerylink:5765:4%%, %%gallerylink:5768:6%%); Cremona a un ponte e a una rimessa per locomotive. Successivamente Maurice Koechlin¹⁷ (1856-1946), allievo di Culmann a Zurigo, con l’ausilio della statica grafica determinò gli sforzi nelle aste della Tour Eiffel, nel ponte ad arco metallico di Garabit nel Cantal¹⁸ e per l’armatura metallica reticolare della statua della Libertà a New York (figure %%gallerylink:5763:2%%,%%gallerylink:5766:5%%,%%gallerylink:5769:7%%).

Nella trentasettesima edizione del Manuale dell’ingegnere di Colombo, il metodo grafico è ampiamente acquisito per il calcolo delle strutture in ferro anche nella pratica professionale. Infatti l’autore scrive a proposito dei ponti a traliccio in ferro: «Dopo aver assegnato ad ogni nodo il peso corrispondente al massimo sforzo interno che si vuol calcolare, questo si determina ordinariamente per via grafica, o con il sistema delle figure reciproche o con metodo di Culmann».¹⁹ 

La continuità didattica è assicurata da una vasta produzione di testi, tra i quali notiamo La Statique graphique. Science introductive à l’art de construire²⁰dove la Statica grafica, chiamata in francese anche Graphostatique, per seguire la traduzione letteraria dal tedesco, non solo è considerata una vera e propria scienza, ma anche propedeutica e indispensabile all’arte del costruire.

La stretta connessione tra scienza, tecnica e società emerge dagli studi di Poncelet che utilizza le nozioni di equilibrio per risolvere per via grafica il problema del calcolo dei ponti sospesi e della forma più conveniente da assegnare a questi. 

Le intenzioni applicative delle teorie alle innovazioni tecnologiche dell’epoca sono evidenti.

Il passaggio dalla trave ad anima piena a quella reticolare prende presumibilmente l’avvio dalla necessità di origine tecnica di realizzarne un alleggerimento dell’anima, con una riduzione del peso proprio e mantenimento di rigidezza flessionale adeguata. Sembra che il criterio seguito fosse basato su singole esperienze come quelle svizzere del secolo XVIII, in cui i fratelli Grubenmann costruiscono il ponte di Sciaffusa, nel 1757, proponendo una struttura ibrida arco-trave.²¹ 

La diffusione dei ponti metallici, prima con travi ad anima piena, secondo l’influenza della vicina scuola francese, poi con il sistema a traliccio, ha luogo con l’avvento della ferrovia (lo stesso Culmann era ingegnere ferroviario).

Un grave incidente avvenuto nel 1891, il collasso del ponte sulla Birse a Münchenstein,²² progettato anch’esso da Eiffel, è all’origine della prima Ordinanza federale del 1892, in virtù della quale tutti i ponti metallici ferroviari devono essere ricalcolati e, se fosse stato il caso, rinforzati. Uno degli esempi più eloquenti in tal senso è relativo al ponte del Kerstelenbach, presso Amsteg, all’imbocco della Val Maderan: il sotto-tirante, caratteristico dei ponti metallici del Gottardo, collaborava con le travi primitive a membrature parallele nel sostenere i carichi. Successivamente la maggior parte dei ponti metallici svizzeri vengono rinforzati poiché, come testimonia l’ingegnere Elskes con le sue statistiche, gli incidenti in tutto il mondo sono numerosi. A tal proposito ci illumina anche una nota sul consolidamento di alcuni ponti metallici, in cui l’autore dichiara che per il rinforzo di ponti con puntone e tiranti all’intradosso, come nell’esempio da lui illustrato sul ponte di Vallorbe, l’uso della statica grafica è più che mai agevole e corretto: «pour un tympan triangulé, la statique graphique permet d’évaluer sans difficulté les efforts de toutes les parties d’une construction de ce genre».²³ 

Nelle note sul collasso dei ponti metallici, soprattutto ferroviari, dovuti all’incremento dei carichi e delle velocità dei convogli, l’ingegnere svizzero Elskes dichiara: «C’était, il est vrai, l’époque où l’on construisait encore, bien que l’argent vînt à manquer, mais c’était aussi et surtout, il faut le reconnaître, la période où s’épanouissaient les méthodes élégantes de la statique graphique et, avec elles, une foi trop aveugle dans l’excellence des calculs et l’infaillibilité de la théorie».²⁴ 

Elskes si riferisce in particolare ai collassi avvenuti tra il 1870 e il 1891, quando la statica grafica è appena «sbocciata» e con quella – afferma – una fede troppo cieca nei confronti dei calcoli e dell’infallibilità della teoria. 

L’impiego dei mezzi grafici nei problemi statici oggi offre molti vantaggi, ma, avendo a priori un campo di applicazione limitato, deve essere adottato in fase di concepimento e progetto di massima della struttura. Per il resto è chiaro che ora il calcolo automatico abbia ormai a ragione preso il sopravvento. Tuttavia in un’ottica di semplificazione, meglio di riduzione della complessità del problema strutturale, i metodi della statica grafica possono ancora essere utilizzati secondo un uso non classico. Le limitazioni imposte dalle ipotesi:
a) che la struttura sia sempre in equilibrio con i carichi esterni, cioè che sia isostatica;
b) che i carichi siano applicati solo ai nodi;
c) che tutti i nodi siano cerniere libere di ruotare;
d) che le linee delle aste si possano confondere con le linee d’asse di tali aste;
e) che le aste si trovino su uno stesso piano,
possono essere superate con l’introduzione di altri principi che ne estendano il campo di applicazione. Tra questi la possibilità di estendere il dominio di applicazione della statica grafica allo studio del comportamento plastico e, sempre in un’ottica di concezione strutturale e non di analisi, alle strutture iperstatiche.

Note

1. R. Secchi, L’architettura è l’arte dell’equilibrio?, "Aperture", 29, 2013.

2. G. Pizzetti, A.M. Zorgno Trisciuoglio, Principi statici e forme strutturali, Utet, Torino 1980.

3. E. Benvenuto, La scienza delle costruzioni e il suo sviluppo

   storico, Sansoni, Firenze 1981.

4. K. Culmann, Die Graphische Statik, Meyer & Zeller, Zürich 1866; 2a ed. vol. 1, 1875; Traité de Statique Graphique, trad. fr. della 2a ed. tedesca di G. Glasser, J. Jacquier, A. Valat, Dunod, Paris 1880.

5. J.V. Poncelet, Cours de mecanique industrielle, exposant les principes de statique et dynamique, les organes mécaniques

   et les moteurs, Leroux, Li.ge 1839.

6. K. Culmann, Die Graphische Statik cit.

7. Simone Stevino Brugensi, Tomus quartus mathematicorum hypomnematum de statica, Leiden 1608 (in Biblioteca del Seminario vescovile di Padova, Italia).

8. P. Varignon, Nouvelle Mecanique, ou Statique, dont le projet fut donné en 1687, t. I, Jombert, Paris 1725 (in Biblioteca

   di Padova, Polo di Ingegneria).

9. Ph. de La Hire, Traité de Mécanique, ou l’on explique tout ce qui est nécessaire dans la pratique des arts, Anisson,

   Paris 1695; reimpr. Compagnie des libraires, Paris 1730.

10. E. Benvenuto, La scienza delle costruzioni cit.

11. D. Tourn.s, Pour une histoire du calcul graphique, "Revue d’histoire des math.matiques", 1, 2000.

12. A. Favaro, La statica grafica nell’insegnamento superiore, Grimaldo, Venezia 1873 (in Biblioteca di Padova, Polo di Ingegneria).

13. K. Chatzis, La reception de la statique graphique en France durant le dernier tiers du XIXe siècle, .Revue d’Histoire des mathematiques., 10, 2004, pp. 7-43.

14. J. Sondericker, Notes on graphic statics, with applications to trusses, beams, and arches, 1896.

15. M. Lévy, La statique graphique et ses applications aux constructions, Gauthier-Villars, Paris 1874.

16. L. Cremona, Le figure reciproche nella statica grafica, Ulrico Hoepli editore, Milano 1879.

17. M. Koechlin, Applications de la statique graphique, Baudry, Paris - Li.ge 1889; 2a ed. 1898.

18. G. Eiffel, Mémoire présenté à l’appui du projet définitif du Viaduc du Garabit, Librairie Polytechnique Baudry et C. .diteurs, Paris - Li.ge, 1889.

19. G. Colombo, Manuale dell’ingegnere civile e industriale, 36a e 37a ed., Ulrico Hoepli editore, Milano 1917, p. 182.

20. A. Pirard, La Statique graphique. Science introductive à l’art de construire, 3a ed., Dunod, Paris 1967.

21. G. Pizzetti, A.M. Zorgno Trisciuoglio, Principi statici e forme strutturali cit.

22. Ch. Lehmann, B. Maurer, Karl Culmann und die Graphische Statik: Zeichnen, die Sprache des Ingenieurs, Ernst & Sohn, Berlin 2006.

23. N. Schoulepnikow, Note sur quelques travaux de consolidation de ponts métalliques, .Bulletin technique de la Suisse romande., 28, 1902.

24. E. Elskes, Rupture des ponts métalliques: étude historique et statistique, .Bulletin de la Soci.t. vaudoise des ing.nieurs et des architectes., 20, 1894.