Géotechnique: méthodes numériques pour la justification aux états-limites ultim
Les règles actuelles de la norme SIA 267 relatives aux justifications aux états-limites ultimes géotechniques sont d’application limitée lorsqu’on utilise des modèles numériques. Cette problématique sera traitée par le futur EC 7 de seconde génération. La commission de normalisation SIA 267 en donne ici un premier aperçu.
Le calcul conventionnel des ouvrages géotechniques se fait habituellement selon la méthode des facteurs partiels définie par l’Eurocode 7 (EC 7) ou la norme SIA 267 Géotechnique. Lorsque le calcul aux états-limites ultimes fait appel à la modélisation numérique, les approches de pondération de la norme SIA 267 sont, de fait, d’application limitée. C’est pour cette raison que diverses études ont été publiées dans la littérature spécialisée au cours de la décennie passée. Elles se sont attachées à montrer les effets de différentes options de pondération lorsqu’elles sont utilisées avec des modèles numériques. L’utilisation spécifique des facteurs partiels dans les modèles numériques sera également traitée par la seconde génération de l’EC 7 à venir. Le présent article donne un aperçu de la manière dont cela devrait se faire.
Contexte
Les éléments essentiels de l’EC 7 et de la norme SIA 267 actuellement en vigueur ont vu le jour à peu près en même temps, il y a une vingtaine d’années. À l’époque, les calculs géotechniques courants faisaient très majoritairement appel aux méthodes analytiques et aux considérations d’équilibre limite. Dans ces deux normes, l’utilisation des facteurs partiels a par conséquent été prévue pour ce type de modèles. Ces derniers temps, le recours à la modélisation numérique (méthode des éléments finis, par exemple) pour le calcul courant des ouvrages géotechniques est devenu de plus en plus fréquent. Si l’utilisation de modèles numériques est bien compatible avec le cadre de l’EC 7 et de la norme SIA 267 pour les états-limites de service (ELS), cela est moins clair pour les états-limites ultimes (ELU). En effet, les normes exigent la multiplication de certaines grandeurs par des facteurs partiels. Or les logiciels de modélisation numérique ne le permettent que sous réserve, ces grandeurs pouvant être par exemple soumises à des conditions d’équilibre. Ceci a conduit à la publication, dans la littérature spécialisée, d’un certain nombre d’études portant sur l’utilisation de différents formats de vérification (voir bibliographie).
Les prochains Eurocodes de seconde génération
Dans le cadre de l’élaboration, au niveau européen, des Eurocodes de seconde génération, la normalisation géotechnique fait actuellement l’objet d’un ajustement en profondeur. La Suisse est également impliquée, au travers de la commission de normalisation SIA 267 pour la géotechnique. Comparée à la première génération, la seconde génération de l’EC 7 aura une plus grande influence sur tout ce qui concerne la géotechnique en Suisse. Le projet de norme actuel comporte diverses nouveautés, dont certaines portent notamment sur la problématique abordée ici. Les explications qui suivent s’appuient sur la version d’août 2022 soumise à consultation.
Présentation sommaire des approches de pondération de l’EC 7 pour les méthodes numériques
Nous livrons ici, sur la base de la version actuelle du projet du nouvel EC 7, déjà bien avancé, une vue d’ensemble des futures méthodes de pondération aux ELU qui y sont proposées. Les sections du nouvel EC 7 concernant les méthodes numériques ont toutes un caractère de recommandation. Pour le calcul conventionnel, la pondération des grandeurs représentatives continue à se faire en appliquant les facteurs partiels aux propriétés de résistance au cisaillement – approche MFA (Material Factoring Approach) –, aux résistances globales – approche RFA (Resistance Factoring Approach) – ou aux effets des actions – approche EFA (Effect-of-Action Factoring Approach).
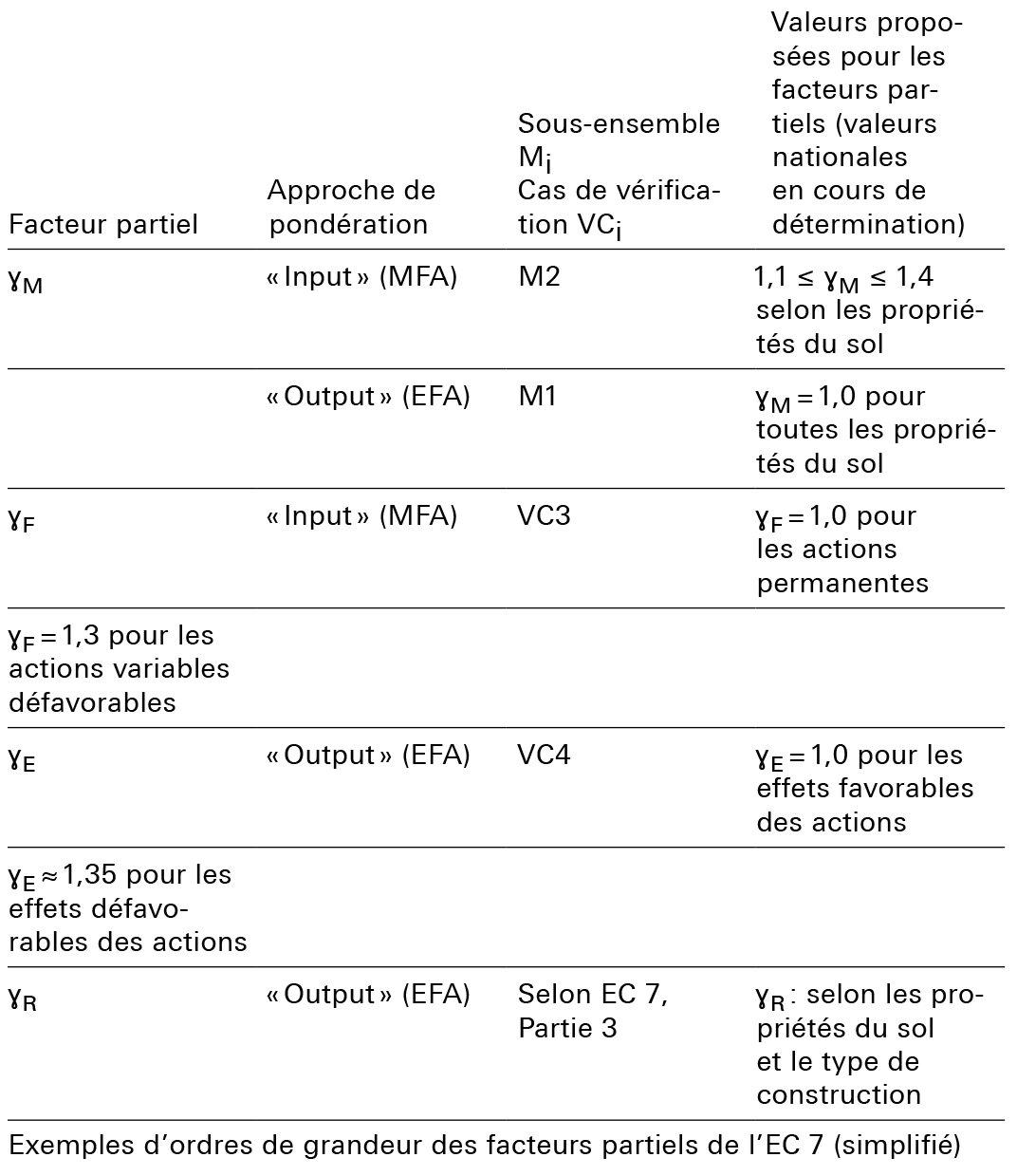
Dans le cas de la modélisation numérique, l’EC 7 recommande l’utilisation des approches MFA (en référence aux modèles numériques, l’EC 7 parle alors d’une approche « input ») et EFA (l’EC 7 parle alors d’une approche «output») – voir les tableaux 1 et 2. Les facteurs partiels intervenant différemment, le calcul est à effectuer selon les deux approches. La vérification selon l’une d’elles peut être omise si l’autre est clairement plus défavorable.
Dans l’approche «input» (MFA), les facteurs partiels pour les propriétés de résistance des sols sont appliqués aux paramètres d’entrée et leurs valeurs numériques sont celles de l’ensemble M2. Les actions sont combinées en utilisant les facteurs correspondant au cas de vérification VC3. Dans cette approche, l’EC 7 décrit deux méthodes :
- pondération avec procédure de réduction de la résistance au cisaillement : les propriétés de résistance du sol sont réduites progressivement jusqu’à atteindre la valeur de calcul ;
- pondération à la source : le calcul est effectué pour les valeurs pondérées des paramètres de résistance.
Dans l’approche «output» (EFA), les facteurs partiels sont appliqués en post-traitement à l’effet des actions (sollicitation) calculé par le modèle. Les valeurs numériques des facteurs partiels pour les propriétés intrinsèques de résistance des sols sont celles de l’ensemble M1, soit gM = 1,0. Une fois le calcul aux éléments finis achevé, on en déduit les valeurs de calcul des sollicitations en utilisant les facteurs partiels correspondant au cas de vérification VC4, soit pour les effets défavorables des actions gE ≈ 1,35 et pour les effets favorables gE = 1,0. Une variante, pour la vérification aux ELU sur la base de modèles numériques, consiste à appliquer le facteur partiel gE aux effets des actions pour le cas de vérification VC4 et le facteur partiel gR à la résistance.
Conclusion
Avec la procédure actuelle définie par l’EC 7, qui cadre en partie avec les approches déjà utilisées concrètement aujourd’hui, on dispose d’une recommandation normative pour l’intégration des facteurs partiels dans les méthodes numériques. Divers cas pratiques pourront ainsi être traités sur une base commune. On notera cependant que, en particulier lorsque les lois de comportement des sols sont complexes, l’interprétation et le jugement de l’ingénieur·e restent indispensables.
Bibliographie
Bond, A. & Harris, A. (2008). Decoding Eurocode 7. Taylor & Francis, Milton Park, United Kingdom.
Deutsche Gesellschaft für Geotechnik DGGT, (2014). Empfehlungen des Arbeitskreises Numerik in der Geotechnik – EANG. Wilhelm Ernst & Sohn, Berlin, Germany.
Estaire, J., Arroyo, M., Scarpelli, G. & Bond, A.J. (2019). Tomorrow’s geotechnical toolbox: Design of geotechnical structures to EN 1997:202x. Proc. of. XVII ECSMGE-2019, pp. 1-8.
Heibaum, M. & Herten, M. (2009). Geotechnical verification using the finite-element method? Bautechnik Special issue 2009 – Geotechnical Engineering. Ernst & Sohn Verlag für Architektur und technische Wissenschaften GmbH & Co, Berlin, pp. 7 – 15.
Herten, M. (2013). EC 7 – Welches Nachweisverfahren ist das Richtige? Workshop «Bemessen mit numerischen Methoden», Veröffentlichungen des Instituts für Geotechnik und Baubetrieb, TU Hamburg-Harburg, Nr. 27, pp.1-11.
Katsigiannis, G., Ferreira, P. & Fuentes, R. (2014). Ultimate Limit state design of retaining walls with numerical methods. 8th European Conference on Numerical Methods in Geotechnical Engineering, Delft, the Netherlands.
Lees, A.S. (2017). Use of geotechnical numerical methods with Eurocode 7. Engineering and Computational Mechanics 170, No. EM4, pp. 146-153.
Potts, D.M. & Zdravkovic, L. (2012). Accounting for partial material factors in numerical analysis. Géotechnique 62, No. 12, pp. 1053-1065.
Schweiger, H.F. (2014). Influence of EC7 design approaches on the design of deep excavations with FEM. Geotechnik 37, Heft 3, pp.169-176.
Smith C. & Gilbert, M. (2011). Ultimate Limit State design to Eurocode 7 using numerical methods Part I: methodology and theory. Ground Engineering, November, pp. 24-29.
Smith C. & Gilbert, M. (2011). Ultimate Limit State design to Eurocode 7 using numerical methods Part II: Proposed design procedure and application. Ground Engineering, October, pp. 25-30.
v. Wolffersdorff, P.-A. (2008). Wie soll die FEM in geotechnische Bemessungsvorschriften einfliessen? Workshop «Bemessen mit Finite-Elemente-Methode» TU Hamburg-Harburg, Veröffentlichung des Instituts für Geotechnik, Nr. 14, pp.133-144.