La ri­cer­ca di for­me strut­tu­ra­li in­no­va­ti­ve

L’adozione del computer come strumento generativo ha trasformato il panorama della progettazione ingegneristica e architettonica, inaugurando nuove possibilità per la ricerca e l’ottimizzazione di forme strutturali innovative. A partire dagli anni Sessanta del secolo scorso, diversi metodi computazionali sono stati sviluppati grazie alle esperienze con modelli fisici da parte di pionieri come Heinz Isler, Frei Otto e Sergio Musmeci. Questi metodi hanno gettato le basi per lo sviluppo di approcci parametrici negli ultimi decenni, esercitando un’influenza significativa sull’introduzione dell’intelligenza artificiale nelle tecniche di progettazione strutturale contemporanee.

Nuove forme strutturali

La definizione della forma strutturale è uno degli aspetti che influenza maggiormente la progettazione degli edifici di grande luce. Non solo ha un impatto sulla materializzazione degli elementi portanti, ma anche sulla qualità dello spazio architettonico. Nelle discipline dell’ingegneria e dell’architettura, il processo che porta all’individuazione di una forma in equilibrio statico in relazione a determinati carichi e condizioni al contorno è definito form finding. Il termine sottolinea come la forma della struttura emerga direttamente dal processo progettuale: una struttura che si attiva nella sua configurazione formale come risposta alla distribuzione delle forze esterne e interne. A differenza della pratica ingegneristica convenzionale in cui le tensioni interne di una struttura vengono calcolate sulla base di una forma predeterminata, questo metodo consente una integrazione esplicita tra forma e comportamento strutturale.

Il form finding trae le sue origini dall’uso di modelli fisici.¹ Gli studi di Robert Hooke (1635-1703) sull’inversione della curva catenaria hanno influenzato il lavoro di Christopher Wren (1632-1723) per il progetto della cupola della Cattedrale di Saint Paul a Londra all’inizio del Settecento e quello di Antoni Gaudì (1852-1926) sulla combinazione di curve catenarie per la progettazione di varie strutture in compressione tra l’Ottocento e il Novecento. D’altra parte, l’esplorazione di strutture principalmente sollecitate in tensione trova le proprie radici negli studi di Leonhard Euler (1707-1783) e Joseph Plateau (1801-1883) sulle pellicole di sapone. Il consolidamento dei metodi di form finding e la loro applicazione in architettura si deve essenzialmente al lavoro di Heinz Isler (1926-2009), Frei Otto (1925-2015) e Sergio Musmeci (1926-1981) nella seconda metà del Novecento.² Essi non solo hanno formalizzato il form finding come disciplina per la progettazione concettuale delle strutture, ma hanno anche aperto la strada allo sviluppo dei primi metodi computazionali.

Il lavoro di Isler si è prevalentemente basato sull’esplorazione di diverse opzioni progettuali realizzate con modelli fisici per la ricerca della forma e per la verifica del comportamento strutturale.³ Nonostante durante la sua carriera abbia visto la progressiva comparsa dei metodi digitali, Isler ha sempre manifestato avversione nei confronti dell’impiego del calcolo assistito dal computer per la fase di form finding. La sua estesa esperienza con i modelli fisici gli permetteva infatti un controllo più immediato sulla forma rispetto a qualsiasi modellazione sul computer. Il confronto tra l’uso del modello fisico e il modello digitale si è concretizzato definitivamente nell’ambito del progetto per la nuova stazione di Stoccarda, caratterizzata da strutture a forma di calice in calcestruzzo armato, dove Isler è stato coinvolto come esperto per la valutazione della configurazione strutturale insieme a Otto.⁴ In quest’occasione Isler ha usato modelli fisici per esplorare soluzioni alternative a quelle sviluppate con metodi numerici dallo studio di ingegneria britannico Buro Happold. A causa delle eccessive approssimazioni dell’algoritmo di calcolo utilizzato, il risultato del modello digitale si discostava molto dalle geometrie dei suoi modelli ottenuti col metodo di form finding fisico della membrana appesa e dagli studi con le pellicole di sapone eseguiti in parallelo da Otto, trovando conferma di quanto aveva annotato una decina d’anni prima: la semplicità ingannevole dei processi digitali può portare a risultati arbitrari.⁵ Tuttavia, studi recenti hanno rivelato che questi strumenti sono stati ampiamente impiegati nella sua pratica ingegneristica.⁶

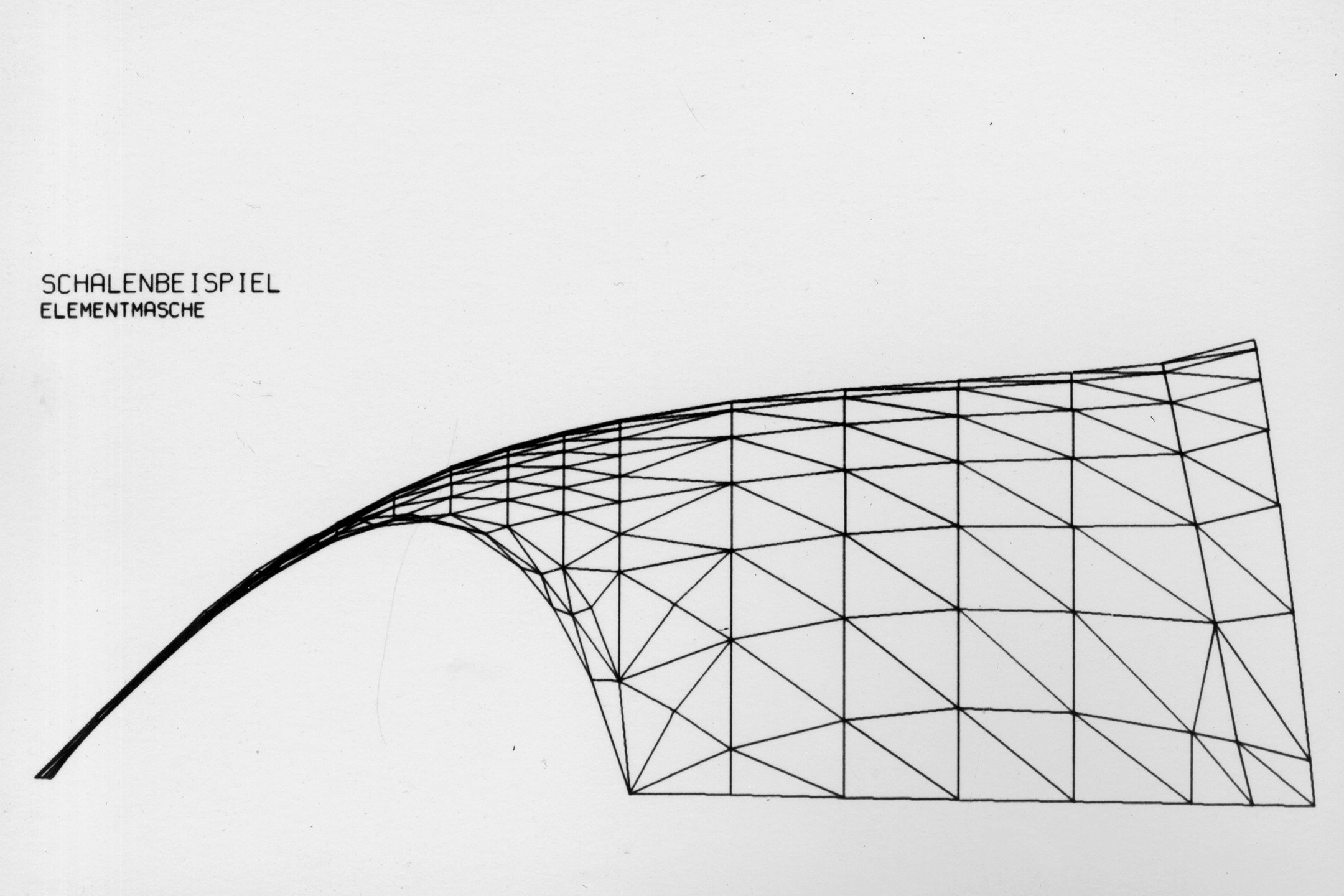
Isler ha utilizzato le tecnologie digitali principalmente per automatizzare calcoli ripetitivi, risparmiando tempo e costi nella redazione della documentazione tecnica necessaria per l’approvazione dei progetti in Francia e Germania. Mentre in Svizzera l’uso del modello fisico era riconosciuto dalle normative tecniche come strumento valido per la verifica del comportamento strutturale,⁷ in altri Stati era richiesto di depositare una relazione di calcolo dettagliata. In questi casi, Isler adottava il metodo agli elementi finiti per la verifica del comportamento strutturale delle strutture di forma libera ottenute da processi di form finding fisico, come nel caso del teatro di Stetten auf den Fildern (1976). (figg. 1-2)

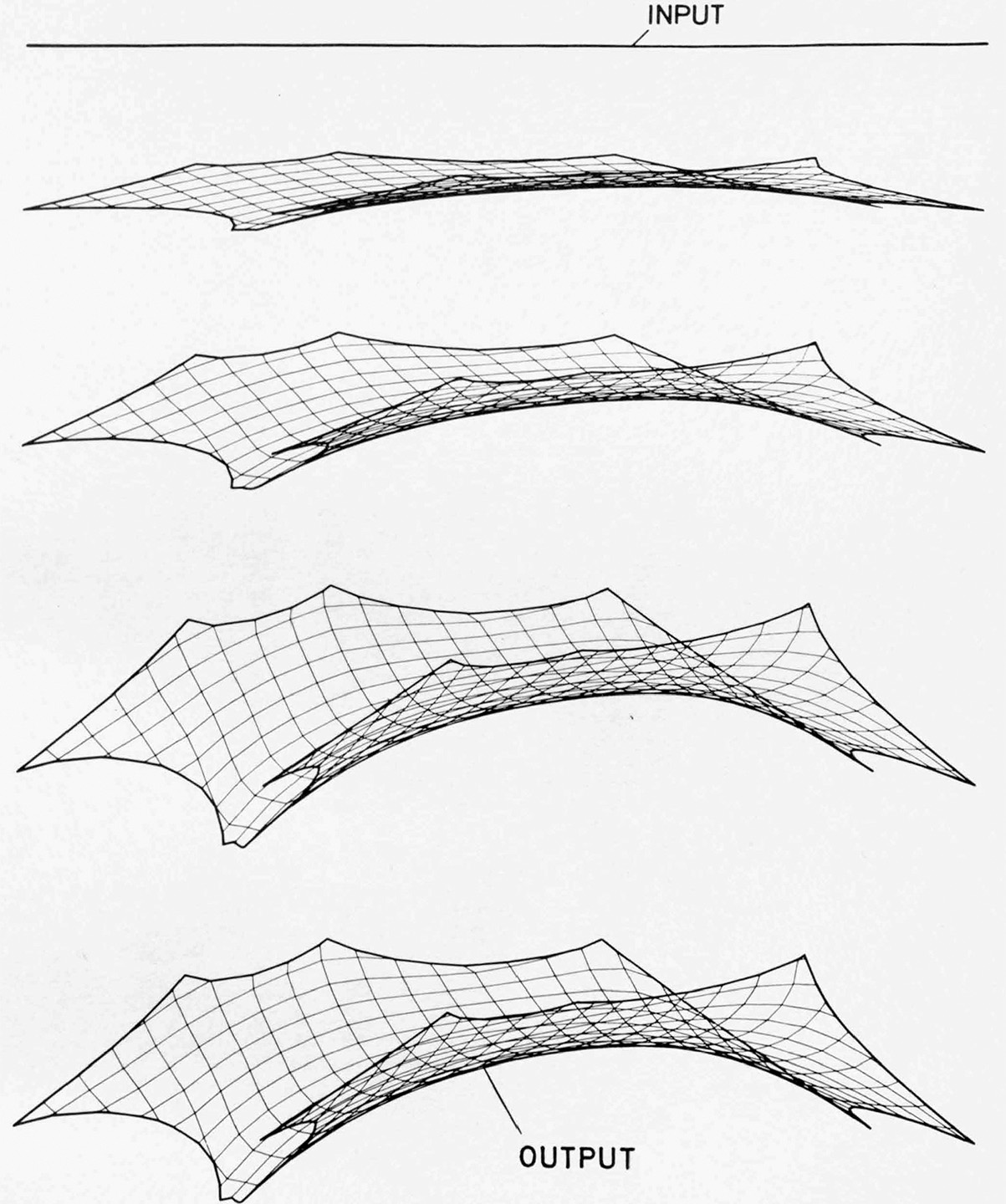
Se Isler ha per lo più prediletto metodi fisici per la progettazione concettuale delle sue strutture, Otto ha esplorato diversi approcci per la creazione e il controllo di nuove forme all’interno del suo gruppo di ricerca presso l’Università di Stoccarda. Il contesto accademico in cui la sua attività era inserita ha favorito ricerche scientifiche estremamente multidisciplinari. L’apertura nei confronti delle nuove tecnologie per la progettazione delle strutture si è anche tradotta nell’uso combinato di metodi fisici e digitali.⁸ Un esempio notevole in questo contesto è il progetto per la copertura dello Stadio Olimpico di Monaco, dove per la prima volta la forma di un modello fisico è stata confrontata e verificata con quella generata dai primi strumenti digitali (figg. 3-4).9 Da un lato, la geometria è stata generata tramite metodi computazionali sviluppati presso l’Istituto per le Applicazioni della Geodesia all’Ingegneria (Institut für Anwendungen der Geodäsie im Bauwesen), diretto da Klaus Linkwitz (1927-2017), tra cui in particolare l’innovativo Force Density Method.¹⁰ Dall’altro, il comportamento strutturale è stato analizzato usando i primi strumenti digitali basati sul metodo agli elementi finiti e specificamente adattati per strutture costituite da reti di cavi e membrane.¹¹

Al contrario di Isler e Otto, l’approccio di Musmeci alla progettazione concettuale delle strutture si fondava su una conoscenza rigorosa della matematica, caratteristica distintiva della scuola italiana di ingegneria.¹² Esso poneva la forma della struttura come l’elemento incognito del processo di progettazione, in maniera simile a Isler con i suoi metodi di form finding fisico e Otto con i suoi approcci ibridi.¹³ La forma emergeva da considerazioni statiche e illustrava in modo immediato le variazioni delle sollecitazioni interne alla struttura. Mentre Isler si è concentrato su forme a guscio in compressione e Otto su membrane in tensione, Musmeci ha esplorato una varietà di tipologie strutturali, dalle strutture piegate, alle superfici continue, fino a strutture reticolari spaziali.¹⁴ (figg. 5-6)

L’approccio matematico alla progettazione strutturale ha permesso a Musmeci di apprezzare le potenzialità offerte dai primi strumenti digitali nell’ingegneria, andando oltre la semplice analisi di forme predefinite.¹⁵ In questo modo, Musmeci ha intuito la possibilità di controllare simultaneamente molteplici parametri, facilitando così l’esplorazione di diverse soluzioni strutturali e ampliando le opportunità di innovazione nella progettazione.¹⁶ Allo stesso tempo, ha immaginato una sinergia tra uomo e macchina in grado di esaltare la creatività nel processo progettuale. Ha previsto che l’introduzione di strumenti digitali fin dalla fase concettuale potesse generare nuove forme architettoniche e strutture innovative. In questo scenario, il ruolo del progettista sarebbe stato quello di selezionare la configurazione strutturale più idonea alle esigenze del progetto, scegliendo tra una moltitudine di possibili alternative progettuali. La sua visione non era così lontana dalla realtà.

L’uso del computer come strumento creativo nella progettazione strutturale

Le sperimentazioni di Isler, Otto e Musmeci hanno rappresentato una pietra miliare nello sviluppo di metodi di progettazione strutturale assistiti da tecnologie informatiche. Dall’inizio degli anni Sessanta, le loro innovazioni hanno stimolato un interesse crescente tra i progettisti nei confronti del form finding digitale, favorito dall’introduzione di nuovi strumenti di calcolo automatico per la progettazione concettuale delle strutture, tra cui il già citato Force Density Method. La definizione di questi primi metodi di calcolo ha inaugurato una fase di sviluppi continuativi, culminati nell’elaborazione di tecniche di form finding digitale sempre più raffinate, rivoluzionando il campo della progettazione strutturale. Tra i contributi significativi emergono il Dynamic Relaxation,¹⁷ l’Updated Reference Strategy, ¹⁸ il Particle Spring System,¹⁹ la Thrust Network Analysis,²⁰ la Vector-based Graphic Statics²¹ e il Combinatorial Equilibrium Modelling.²² 

Negli ultimi anni, la combinazione tra form finding digitale e modellazione parametrica si è dimostrata un metodo estremamente efficace nel campo della progettazione strutturale. Questa sinergia permette di correlare direttamente parametri geometrici relativi alla forma delle strutture con le loro prestazioni meccaniche, quali sollecitazioni interne e capacità portante, fornendo la possibilità di valutare in tempo reale l’impatto delle variazioni di tali parametri sul comportamento strutturale. Utilizzando funzioni matematiche e relazioni geometriche, questa tecnica non solo agevola l’ottimizzazione della geometria delle strutture migliorandone efficienza e stabilità, ma facilita anche l’esplorazione di geometrie complesse, espandendo significativamente le possibilità di innovazione nella progettazione. L’impiego di tecniche di form finding digitale all’interno di ambienti di progettazione parametrica, come la nota piattaforma Rhinoceros 3D e il suo plug-in di programmazione visuale Grasshopper, ha aperto agli ingegneri e agli architetti nuove prospettive per sfruttare il potenziale creativo dei computer nella creazione di forme strutturali innovative.²³ 

In questo contesto, la statica grafica come strumento computazionale parametrico ha suscitato recentemente un rinnovato interesse sia nel campo professionale che in quello accademico. La statica grafica consiste in una serie di costruzioni geometriche che mettono in relazione la forma di una struttura in equilibrio statico con le forze che agiscono su di essa. Questo approccio si avvale dell’uso di due diagrammi reciproci: il diagramma della forma, che mostra la geometria della struttura unitamente alle forze esterne applicate, e il diagramma delle forze (o cremoniano), che costituisce una rappresentazione vettoriale dell’equilibrio delle forze esercitate su ogni nodo della struttura attraverso poligoni delle forze. A seguito della sua formalizzazione come disciplina indipendente nella seconda metà dell’Ottocento a opera di William Rankine (1820-1872), Karl Culmann (1821-1881), Luigi Cremona (1830-1903) e James Clerk Maxwell (1831-1879), la statica grafica è stata ampiamente adottata da ingegneri e architetti per l’analisi e la progettazione strutturale, prima di essere gradualmente soppiantata dall’introduzione dei metodi analitici nella prima metà del Novecento.²⁴ Un esempio emblematico del suo uso si trova nell’opera di Robert Maillart (1872-1940), che impiegò la statica grafica per la progettazione di vari ponti in calcestruzzo armato, tra cui il celebre ponte Salginatobel a Schiers (1928-1930).²⁵ L’evoluzione degli strumenti informatici degli ultimi anni ha svolto un ruolo cruciale nella riscoperta della statica grafica e nella sua implementazione come strumento digitale parametrico. In particolare, la capacità di controllare e visualizzare il flusso delle forze nello spazio ha elevato la statica grafica computazionale a strumento essenziale nell’ambito della progettazione strutturale, consentendo al progettista di affrontare problemi complessi che non possono essere risolti efficacemente solo con metodi basati sul calcolo numerico.

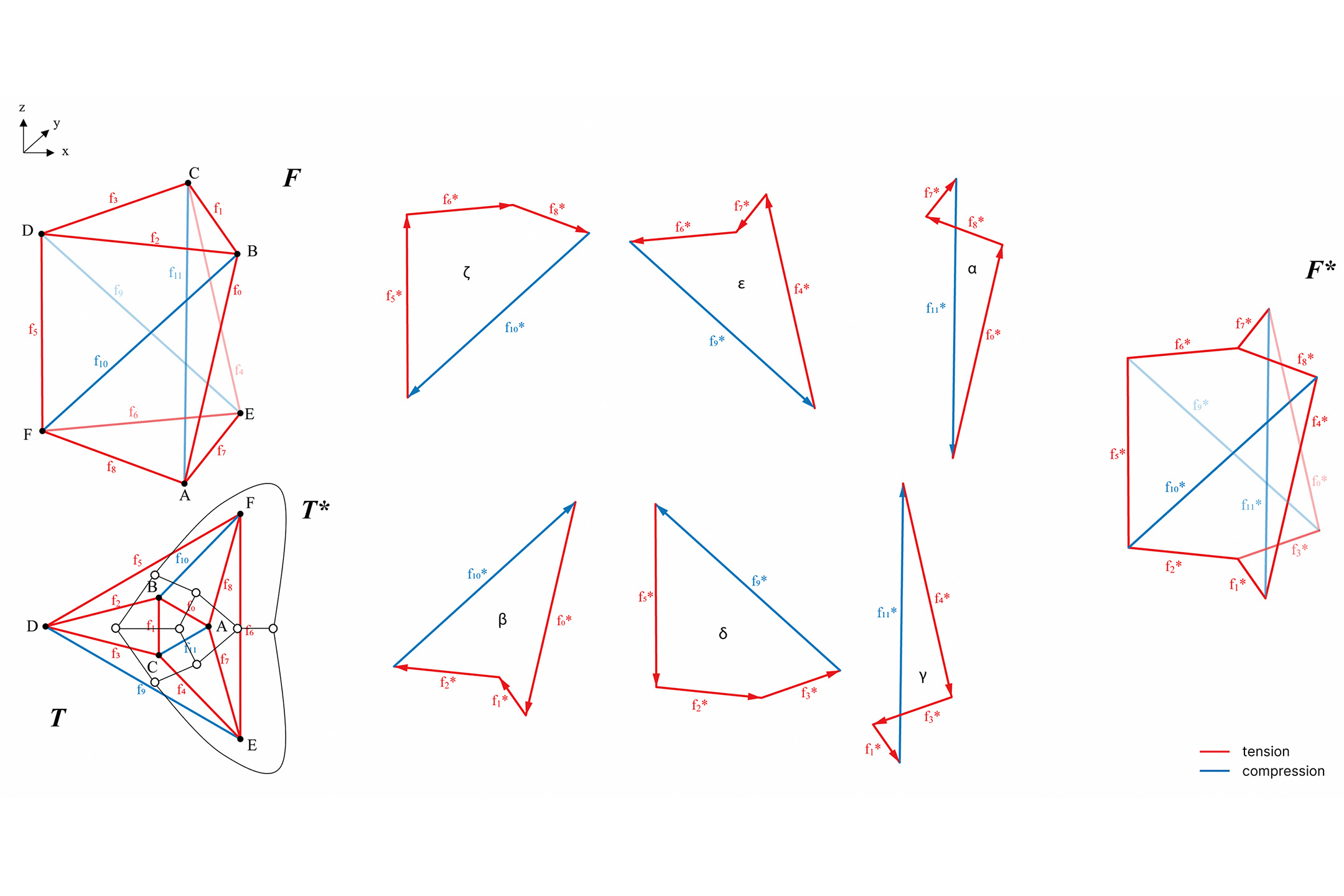
Tra le recenti riproposizioni della statica grafica in ambito digitale,²⁶ la Vector-based Graphic Statics (VGS) si propone come un versatile strumento di progettazione strutturale nella fase concettuale, grazie alla possibilità di operare su strutture tridimensionali complesse in maniera intuitiva. Sviluppata come un’estensione tridimensionale della statica grafica tradizionale bidimensionale, VGS si basa sull’uso di diagrammi della forma e delle forze tridimensionali costituti da vettori (fig. 7). Dal punto di vista topologico, questi diagrammi si distinguono per una dualità tridimensionale, che si manifesta nel parallelismo tra i lati corrispondenti dei due diagrammi e nella correlazione tra i nodi nel diagramma della forma e i poligoni delle forze nel diagramma delle forze. Questa configurazione è in linea con i diagrammi bidimensionali di Cremona, estendendone l’applicazione e la comprensione allo spazio tridimensionale. Nonostante la mancanza di una reciprocità rigorosa tra i diagrammi vettoriali tridimensionali nella VGS, la loro applicabilità nella progettazione strutturale e nel form finding è assicurata dalla capacità di mantenere la dualità tra elementi corrispondenti tra i due diagrammi durante le trasformazioni geometriche, preservando le relazioni fondamentali tra le forze e le forme strutturali.

Durante la fase progettuale, l’interdipendenza tra i diagrammi permette di apportare modifiche a uno dei due diagrammi e osservare immediatamente l’impatto visivo sull’altro diagramma. Ad esempio, questa proprietà fornisce al progettista la flessibilità di alterare la geometria della struttura tramite il diagramma delle forme, valutando in tempo reale l’effetto di tali cambiamenti sulla distribuzione delle forze nell’altro diagramma. Viceversa, è possibile modificare la distribuzione delle forze nel diagramma delle forze e vedere come queste modifiche influenzano la geometria della struttura nel diagramma delle forme.

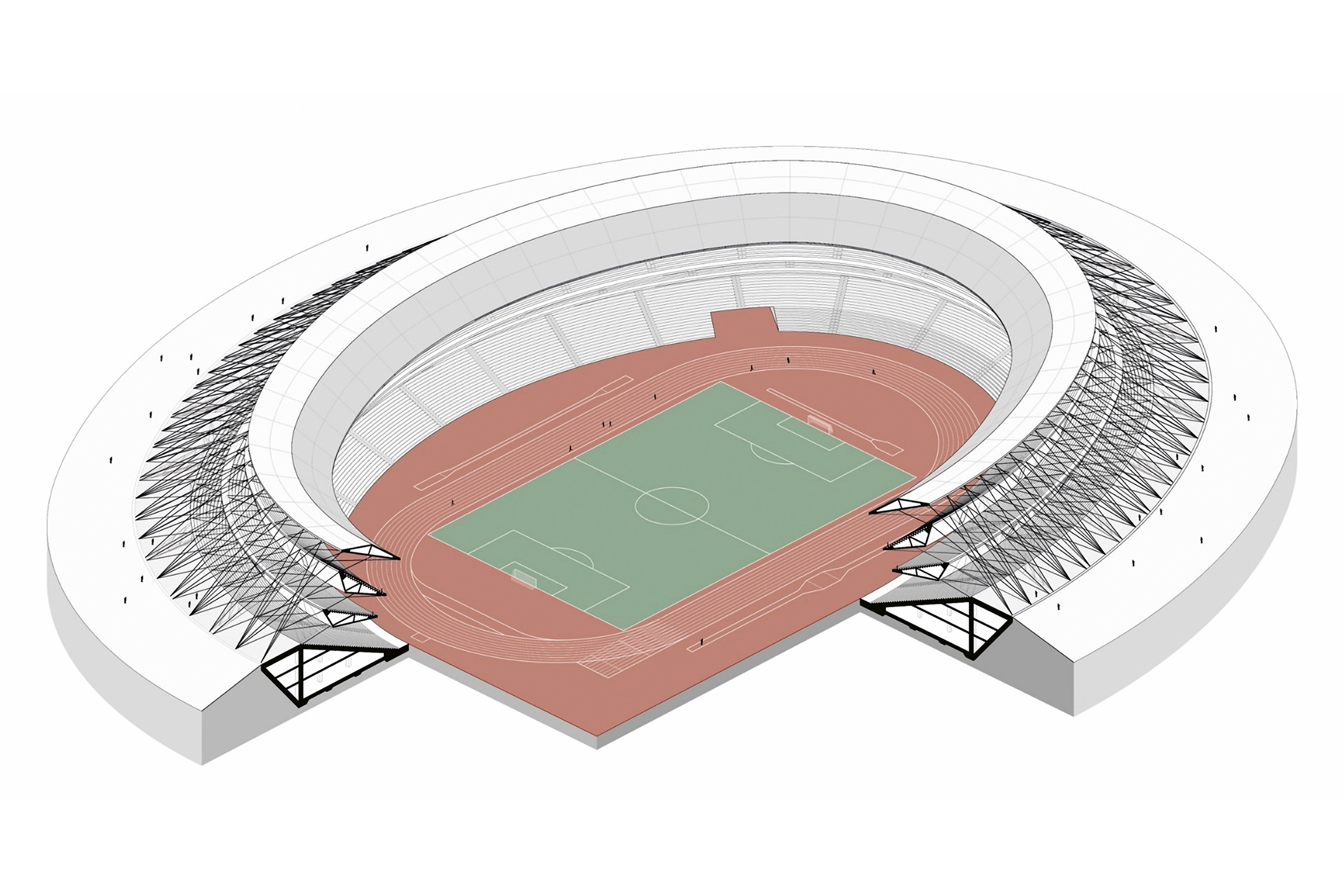
Includendo un diagramma topologico in combinazione con i diagrammi di forma e delle forze, il Combinatorial Equilibrium Modelling (CEM) consente di esplorare in modo parametrico e interattivo varie forme strutturali in equilibrio statico per combinazioni topologiche variabili di forze di tensione e compressione all’interno degli elementi strutturali. Nel CEM, l’equilibrio della struttura è soddisfatto come precondizione durante il processo di form finding. Di conseguenza, le strutture ottenute tramite CEM risultano sempre in equilibrio, anche nei casi in cui le condizioni al contorno imposte dal problema non possono essere completamente soddisfatte. Questa peculiarità consente potenzialmente anche ai progettisti inesperti di comprendere come gli aspetti architettonici e strutturali del progetto si uniscano nel processo di form finding. Nel CEM, i parametri di input sono definiti in unità fisiche assolute, come lunghezze delle barre che compongono la struttura e le intensità delle forze interne a questi elementi. Questo approccio rende il processo più intuitivo e diretto rispetto ad altri metodi, come il Force Density Method in cui i parametri di input sono espressi come rapporti astratti di densità di forza per lunghezza che mancano di una interpretazione fisica diretta. La mappatura diretta tra i parametri di input e la forma risultante in equilibrio è particolarmente utile nella fase iniziale della progettazione, quando gli obiettivi e i vincoli del problema progettuale non sono ancora completamente definiti. Un esempio di struttura innovativa progettata con CEM è rappresentato dalla proposta per il nuovo Stadio Olimpico di Tokyo 2020 (figg. 8-9), in cui la configurazione tradizionalmente adottata nel design degli stadi è stata rivista, portando alla creazione di una soluzione strutturale innovativa. In questa proposta concettuale, tre anelli (due configurati come tribune e uno come copertura) sembrano fluttuare nell’aria, sovrapposti l’uno all’altro come elementi solidi.²⁷ La rete di cavi pretesi impiegata per sostenere questi anelli fluttuanti crea un filtro semi-permeabile tra l’interno e l’esterno dello stadio, generando una piazza pubblica attorno alle tribune.

Gli sviluppi più recenti nel settore della progettazione strutturale assistita da computer indicano l’importanza crescente dell’intelligenza artificiale (AI). Questa tecnologia sta rivoluzionando il campo della progettazione architettonica e strutturale, facilitando un’interazione sinergica tra la creatività umana e l’avanzata capacità computazionale dei computer.²⁸ Gli algoritmi di AI, tra cui le reti neurali artificiali che apprendono in modo autonomo analizzando vasti set di dati di input e output, sono in grado di identificare correlazioni complesse all’interno dei dati, consentendo ai modelli di effettuare previsioni e generalizzazioni con elevata precisione. Uno degli aspetti più vantaggiosi dell’AI è la sua efficacia nel semplificare la gestione di problemi di progettazione complessi, multi-parametrici e altamente non lineari. Questa capacità si rivela fondamentale nella progettazione strutturale parametrica, dove spesso emerge un conflitto tra la ricerca di diversità nello spazio delle soluzioni e la difficoltà del progettista di gestire grandi volumi di dati. In questo contesto, l’AI offre un supporto prezioso ai progettisti nella ricerca sistematica di nuove configurazioni strutturali durante la fase di concettualizzazione, consentendo loro di spingersi oltre i confini delle tipologie strutturali tradizionali pur senza perdere il controllo sui vari parametri di progetto. Un metodo promettente in questo ambito è la Self-Organizing Map (SOM), una tecnica avanzata di apprendimento automatico non supervisionato che si dimostra particolarmente efficace nel convertire uno spazio di soluzioni multidimensionale in una rappresentazione bidimensionale, facilitando così l’analisi visuale e l’interpretazione dei dati da parte del progettista. In combinazione con tecniche di progettazione strutturale come VGS o CEM descritte precedentemente, SOM consente l’esplorazione di molteplici soluzioni alternative (fig. 10) durante la fase progettuale concettuale.²⁹ 

È tuttavia cruciale considerare l’AI non come un sostituto del progettista umano, ma come un sofisticato strumento di supporto alla progettazione. Assicurare un equilibrio ottimale tra le avanzate capacità dell’AI e l’intuizione umana è fondamentale per garantire un’interazione produttiva ed efficace tra tecnologia e creatività. Come affermato da Isler alla fine degli anni Novanta, «soprattutto nel mondo creativo dell’architettura non cubica, il lavoro con l’immaginazione umana e con i modelli fisici (naturali) non solo è prezioso, ma anche altamente superiore. L’automatismo non potrà mai sostituire la mente umana».³⁰

Note

1. B. Addis, Physical Models: Their Historical and Current Use in Civil and Building Engineering Design, Ernst & Sohn, Berlin 2021.

2. G. Boller, P. D’Acunto, Structural Design via Form Finding: Comparing Frei Otto, Heinz Isler and Sergio Musmeci, in J. Mascarenhas-Mateus, A.P. Pires (a cura di), Histories of Construction Cultures Volume 2, CRC Press, Leiden 2021, pp. 431-438.

3. H. Isler, Generating Shell Shapes by Physical Experiments, «Bulletin of the International Association for Shell and Spatial Structures», 1993, n. 34 (1), pp. 53-63.

4. G. Boller, J. Schwartz, Modelling the form. Heinz Isler, Frei Otto and their approaches to form-finding in Proceedings of the 7th Conference of the Construction History Society, Cambridge 2020, pp. 565-576.

5. H. Isler, Letter to David Billington, Documento d’archivio, 1986, 217-02331, gta Archives / ETH Zürich.

6. G. Boller, The model as a working method. Heinz Isler’s experimental approach to shell design, Tesi di dottorato, ETH Zürich, 2022.

7. P. Lardy, Die Neuen S.I.A. - Normen Für Die Bauten in Beton, Eisenbeton Und Vorgespannte Beton, «Schweizerische Bauzeitung», 1955, n. 73 (42), pp. 618-619.

8. G. Vrachliotis, Frei Otto - Denken in Modellen, Spector Books, Leipzig 2019.

9. M. Eekhout, Frei Otto and the Munich Olympic Games, «Zodiac», 1972, n. 21, pp. 12–73.

10. K. Linkwitz, H.J. Schek, Über eine Methode zur Berechnung vorgespannter Seilnetze und ihre praktische Anwendung auf die Olympiadächer München, «IABSE Congress Report», 1972, n. 9, pp. 393-397.

11. J.H. Argyris et al, Higher-order simplex elements for large strain analysis, «Computer methods in applied mechanics and engineering», 1978, n. 16, pp. 369-403.

12. T. Iori, S. Poretti, Ascesa e declino della scuola italiana di ingegneria, in P. Desideri et al. (a cura di), La concezione strutturale. Ingegneria e architettura in Italia negli anni cinquanta e sessanta, Umberto Allemandi & C., Torino 2013, pp. 181-191.

13. S. Musmeci, La Statica e le Strutture, Cremonese, Roma 1971.

14. S. Musmeci, La genesi della forma nelle strutture spaziali, «Parametro», 1979, n. 80, pp. 13-33; P. D’Acunto, L. Ingold, The Approach of Sergio Musmeci to Structural Folding, in Proceedings of the IASS, Tokyo 2016.

15. L. Ingold, Form as the Unknown: Sergio Musmeci - Explorations in the Design of Structures, Tesi di dottorato, ETH Zürich, 2021.

16. S. Musmeci, Strutture nuove per un materiale nuovo, «L’Industria Italiana del Cemento», 1980, n. 5, pp. 345-366.

17. M.R. Barnes, Form Finding and Analysis of Tension Structures by Dynamic Relaxation, «International Journal of Space Structures», 1999, n. 14 (2), pp. 89-104.

18. K.-U. Bletzinger, E. Ramm, A General Finite Element Approach to the form Finding of Tensile Structures by the Updated Reference Strategy, «International Journal of Space Structures», 1999, n. 14(2), pp. 131-145.

19. A. Kilian, J. Ochsendorf, Particle-spring systems for structural form finding, «Journal of the IASS», 2005, n. 46 (147).

20. P. Block, J. Ochsendorf, Thrust Network Analysis: A new methodology for three-dimensional equilibrium, «Journal of the IASS», 2007, n. 48 (3), pp. 167-173.

21. P. D’Acunto et al., Vector-Based 3D Graphic Statics: A Framework for the Design of Spatial Structures Based on the Relation between Form and Forces, «International Journal of Solids and Structures», 2019, n. 167, pp. 58–70.

22. P.O. Ohlbrock, P. D’Acunto, A Computer-Aided Approach to Equilibrium Design Based on Graphic Statics and Combinatorial Variations, «Computer-Aided Design», 2019, n. 121.

23. P.O. Ohlbrock et al., Conceptual design of structures of structures in the digital age, in P. D’Acunto et al. (a cura di), Conceptual Design of Structures: Connecting Engineering and Architecture, Birkhäuser, Berlin, Boston 2024, pp. 80-90.

24. K.E. Kurrer, The History of the Theory of Structures, from Arch Analysis to Computational Mechanics, Ernst & Sohn, Berlin 2008.

25. C. Fivet, D. Zastavni, Robert Maillart’s Key Methods from the Salginatobel Bridge Design Process (1928), «Journal of the IASS», 2012, n. 53(1), pp. 39-47.

26. M. Konstantatou et al., Polarities in structural analysis and design: n-dimensional graphic statics and structural transformations, «International Journal of Solids and Structures», 2018, n. 152–153, pp. 272-293.

27. P.O. Ohlbrock, P. D’Acunto, Tragwerksentwürfe mit Gleichgewichtsmodellen / Structural design with equilibrium models, «Detail Structure», 2019, n. 4, pp. 11-16.

28. P.O. Ohlbrock et al., Conceptual design of structures of structures in the digital age, in P. D’Acunto et al. (a cura di), Conceptual Design of Structures: Connecting Engineering and Architecture, Birkhäuser, Berlin, Boston 2024, pp. 80-90.

29. K. Saldana Ochoa et al., Beyond typologies, beyond optimization: Exploring novel structural forms at the interface of human and machine intelligence, «International Journal of Architectural Computing», 2021, n. 19(3), pp. 466–490.

30. H. Isler, «Is the Physical Model Dead?», in J. Chilton et al., Structural Morphology. Towards the New Millennium, School of Architecture University of Nottingham, Nottingham 1997, p. 170.